Physics and Mathematics
Acceleration
1. Introduction
Acceleration is defined as the rate of change of velocity of a body with respect to time.
A body is said to be accelerated if there is a change in the magnitude or direction of its velocity, or both.
[a = \dfrac{\Delta v}{\Delta t}]
Where:
- [a] = acceleration
- [\Delta v] = change in velocity
- [\Delta t] = time interval during which change occurs
2. Types of Acceleration
- Uniform Acceleration:
When a body’s velocity changes by equal amounts in equal intervals of time, acceleration remains constant.
Example: Free fall of a body under gravity. - Non-Uniform (Variable) Acceleration:
When velocity changes by unequal amounts in equal intervals of time.
Example: A car moving in traffic. - Positive Acceleration:
When velocity increases with time. - Negative Acceleration (Retardation/Deceleration):
When velocity decreases with time.
Example: A moving vehicle coming to rest.
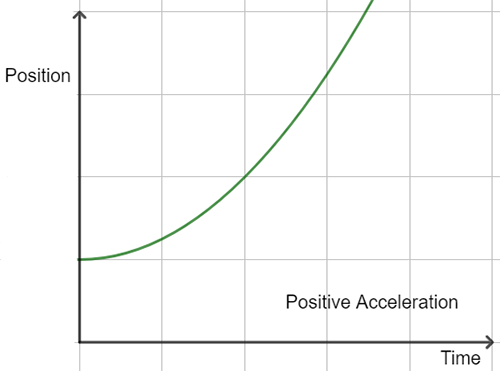
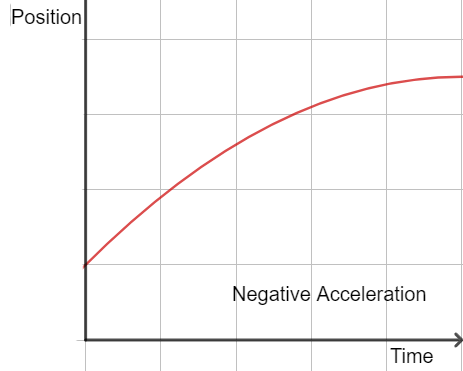
3. Instantaneous Acceleration
When an object is moving with variable acceleration, then the object possesses different accelerations at different instants. The acceleration of the object at a given instant of time or at a given point of motion, is called its instantaneous acceleration.
Consider an object moving with non-uniform acceleration along a straight line. Let $ \displaystyle \overrightarrow{v}$ and $ \displaystyle \overrightarrow{v}+\Delta \overrightarrow{v}$ be the velocities of the object at instants of time $ \displaystyle t$ and $ \displaystyle t+\Delta t$, there $ \displaystyle \Delta t$ is very small time interval. The acceleration of the object at an instant $ \displaystyle t$ i.e., instantaneous acceleration is nearly equal to average acceleration in small time interval $ \displaystyle \Delta t$, because in this time-interval the acceleration of the object can be considered to be uniform, even though the object has non-uniform acceleration.
Therefore, instantaneous acceleration ‘a’ will be approximately equal to average acceleration in small time $ \displaystyle t+\Delta t$ and in given by
$ \displaystyle \overrightarrow{a}=\dfrac{{\Delta \overrightarrow{v}}}{{\Delta t}}$
The sense of approximation in the above expression can be removed by making the time interval $ \displaystyle \Delta t$ tends to zero. Thus, instantaneous acceleration
$ \displaystyle \overrightarrow{a}=\underset{{\Delta t\to 0}}{\mathop{{\lim }}}\,\left( {\dfrac{{\Delta \overrightarrow{v}}}{{\Delta t}}} \right)$
Hence, instantaneous acceleration of an object at a given instant is defined as the limiting value of the average acceleration in a small time interval around the given instant, when the time interval tends to zero.
Therefore, instantaneous acceleration,
$ \displaystyle \overrightarrow{a}=\underset{{\Delta t\to 0}}{\mathop{{\lim }}}\,\left( {\dfrac{{\Delta \overrightarrow{v}}}{{\Delta t}}} \right)=\dfrac{{dv}}{{dt}}$
$ \displaystyle \begin{array}{l}\text{As, }\overrightarrow{v}=\dfrac{{d\overrightarrow{x}}}{{dt}},\text{ therefore,}\\\overrightarrow{a}=\dfrac{d}{{dt}}\left( {\dfrac{{d\overrightarrow{x}}}{{dt}}} \right)=\dfrac{{{{d}^{2}}x}}{{d{{t}^{2}}}}\end{array}$
Thus, instantaneous acceleration of an object is also equal to the second derivative of the position of the object at the given instant.
3. SI Unit and Dimensional Formula
- SI Unit: [m/s²]
- Dimensional Formula: [M^0 L^1 T^{-2}]
4. Key Points
- Acceleration is a vector quantity.
- It depends on the change in velocity and the time interval.
- A body can have acceleration even if speed is constant, provided the direction of velocity changes (e.g., uniform circular motion).
- If there’s no change in velocity, acceleration is zero.
5. Important Formulas to Remember
| No. | Formula | Description |
|---|---|---|
| 1 | [a = \dfrac{\Delta v}{\Delta t}] | Average acceleration |
| 2 | [a = \dfrac{dv}{dt}] | Instantaneous acceleration (Calculus form) |
| 3 | [v = u + at] | First equation of motion (u = initial velocity) |
| 4 | [s = ut + \dfrac{1}{2} a t^2] | Second equation of motion |
| 5 | [v^2 = u^2 + 2as] | Third equation of motion |
| 6 | [a = \dfrac{v^2 – u^2}{2s}] | Acceleration from displacement |
| 7 | [g \approx 9.8 , \text{m/s}^2] | Acceleration due to gravity near Earth’s surface |
6. Practice Questions
- A car’s velocity increases from 10 m/s to 25 m/s in 5 s. Find its acceleration.
Solution: [a = \dfrac{v – u}{t} = \dfrac{25 – 10}{5} = 3 , \text{m/s}^2] - A bike decelerates uniformly from 30 m/s to rest in 6 s. Find its retardation.
Solution: [a = \dfrac{0 – 30}{6} = -5 , \text{m/s}^2] (negative because velocity decreases) - A stone is dropped from rest. Find its velocity after 4 s.
Solution: [v = u + at = 0 + 9.8 \times 4 = 39.2 , \text{m/s}] - An object moving with 12 m/s comes to rest after covering 24 m under uniform retardation. Find the retardation.
Solution: [a = \dfrac{v^2 – u^2}{2s} = \dfrac{0 – 144}{48} = -3 , \text{m/s}^2] - A car moving at 15 m/s accelerates uniformly at 2 m/s². Find the distance covered in 8 s.
Solution: [s = ut + \dfrac{1}{2} a t^2 = 15 \times 8 + \dfrac{1}{2} \times 2 \times 8^2 = 120 + 64 = 184 , \text{m}]
7. Conceptual Questions
1. What is acceleration in simple words?
Acceleration tells us how quickly a body’s velocity changes with time.
2. Can a body have acceleration if its speed remains constant?
Yes. If the direction of velocity changes (like in circular motion), acceleration is present even at constant speed.
3. What does zero acceleration imply?
It means there’s no change in velocity; the object moves with constant velocity or is at rest.
4. Is acceleration always in the direction of velocity?
No. If the body slows down, acceleration acts opposite to the direction of velocity.
5. Can acceleration be negative?
Yes. Negative acceleration (retardation) means velocity decreases with time.
6. What physical quantity does the slope of a velocity–time graph represent?
The slope of the velocity–time graph gives the acceleration.
7. If an object moves in a straight line at 20 m/s for 5 s, is it accelerating?
No. Since velocity is constant, acceleration is zero.
8. What is instantaneous acceleration?
It’s the acceleration of a body at a specific instant of time, found using calculus [a = \dfrac{dv}{dt}].
9. Why is acceleration a vector quantity?
Because it has both magnitude and direction, depending on how velocity changes.
10. Can a stationary object have acceleration?
No. A stationary object with zero velocity cannot have acceleration.
11. If velocity is zero at some instant, is acceleration necessarily zero?
No. At the highest point of a vertically thrown ball, velocity is zero but acceleration due to gravity is still acting.
8. FAQs / Common Misconceptions
1. Does zero acceleration mean zero velocity?
No. Zero acceleration means velocity is constant; it can be zero or non-zero.
2. Can an object have acceleration without moving?
No. Acceleration requires a change in velocity, and velocity requires motion.
3. If a body is moving with negative acceleration, is it always moving backward?
No. Negative acceleration just means it’s slowing down in the forward direction.
4. Can acceleration be constant if velocity is changing?
Yes. Uniform acceleration means velocity changes at a constant rate.
5. If velocity becomes zero at some point, does acceleration also become zero?
Not necessarily. At the highest point of a projectile, velocity is zero but acceleration due to gravity continues.