Physics and Mathematics
Theorem of Parallel Axis
1. Introduction
The Theorem of Parallel Axis helps in finding the moment of inertia [I] of a rigid body about any axis that is parallel to an axis passing through the center of mass (C.M.).
It is particularly useful when the moment of inertia about the C.M. is known, and we need to calculate it about a different axis at some distance away.
2. Statement of the Theorem
If the moment of inertia of a body about an axis passing through its center of mass is [ I_{CM} ], and the new axis is parallel to this axis and at a distance [ h ] from it, then:
[
I = I_{CM} + Mh^2
]
where:
- [ I ] = Moment of inertia about the new axis
- [ I_{CM} ] = Moment of inertia about the axis through the center of mass
- [ M ] = Mass of the body
- [ h ] = Perpendicular distance between the two axes
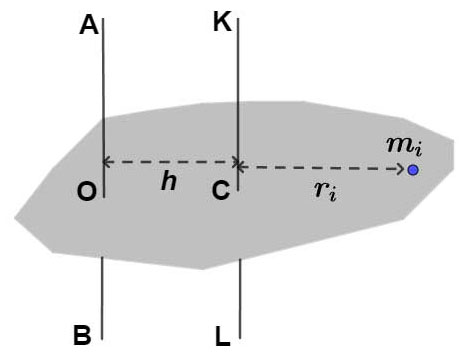
3. Derivation
Let the body consist of many particles, each of mass [ m_i ] at a perpendicular distance [ r_i ] from the axis through the center of mass (C.M.).
If the new axis is at a distance [ h ] from the C.M. axis, then the distance of the particle from the new axis becomes [ r_i’ = r_i + h ].
The moment of inertia about the new axis is:
[
I = \sum m_i (r_i’)^2 = \sum m_i (r_i + h)^2
]
Expanding the term:
[
I = \sum m_i (r_i^2 + 2r_i h + h^2)
]
[
I = \sum m_i r_i^2 + 2h \sum m_i r_i + h^2 \sum m_i
]
Since the origin is at the center of mass, [ \sum m_i r_i = 0 ].
Thus,
[
I = I_{CM} + Mh^2
]
Hence proved.
4. Key Features
- The theorem provides a quick way to find [ I ] about any parallel axis once [ I_{CM} ] is known.
- Applicable to any rigid body, irrespective of its shape.
- Useful for composite or combined objects (e.g., rods, discs, rings).
- Does not depend on the orientation of the axis — only the distance between the axes matters.
5. Important Formulas to Remember
| Quantity | Formula | Description |
|---|---|---|
| Moment of inertia about new axis | [ I = I_{CM} + Mh^2 ] | Parallel axis theorem |
| Distance between axes | [ h] [= \text{perpendicular distance between axes} ] | |
| Moment of inertia about C.M. axis | [ I_{CM} = I – Mh^2 ] | Rearranged form |
6. Conceptual Questions
1. What does the parallel axis theorem relate?
It relates the moment of inertia about any axis to that about a parallel axis through the center of mass.
2. Does the theorem apply to rotational axes not parallel to each other?
No, it applies only to axes that are parallel to each other.
3. What happens if the distance [ h = 0 ]?
The new axis coincides with the C.M. axis, so [ I = I_{CM} ].
4. Why does the term [ 2h \sum m_i r_i ] vanish?
Because the origin is at the center of mass, hence [ \sum m_i r_i = 0 ].
5. What is the physical meaning of the term [ Mh^2 ]?
It represents the additional moment of inertia due to the shift of the axis by distance [ h ] from the C.M.
6. Can this theorem be applied to continuous bodies?
Yes, by replacing the summation with integration.
7. What is the parallel axis theorem for a uniform rod?
For a rod of length [ L ], about an axis through one end, [ I = \dfrac{1}{12}ML^2 + M\left(\dfrac{L}{2}\right)^2 = \dfrac{1}{3}ML^2 ].
8. Why is the theorem useful in calculating rotational kinetic energy?
Because it allows computing [ I ] about any required rotation axis without complex integration.
9. Does the theorem depend on the shape of the body?
No, it is universally valid for all rigid bodies.
10. Can we derive the perpendicular axis theorem using this theorem?
No, they are independent theorems that apply to different geometrical setups.
7. FAQ / Common Misconceptions
1. Is the parallel axis theorem valid for non-rigid bodies?
No, it assumes the body is rigid; internal deformation invalidates it.
2. If we shift the axis through C.M. by distance [ h ], does [ I_{CM} ] change?
No, [ I_{CM} ] is a fixed property about the C.M. axis and doesn’t change with the shift.
3. Does the mass of the body affect the additional term [ Mh^2 ]?
Yes, a larger mass increases the added inertia proportionally.
4. Is the theorem derived from experimental observation?
No, it’s purely mathematical, derived from the definition of moment of inertia.
5. Does the theorem apply if axes intersect?
No, it only applies to **parallel** axes; intersecting ones require a different analysis.