Physics and Mathematics
Moment on Inertia of a Thin Circular Ring
Consider a ring of mass $M$, radius $R$ and center $O$. Then, mass per unit length of the circumference of the ring $= \dfrac{M}{2 \pi R}$
Moment of inertia about an axis through its center and perpendicular to its plane
Let the moment of inertia of the circular ring about the axis $ZZ’$ passing through its center $O$ and perpendicular to its plane. Consider an elementary portion of the ring.
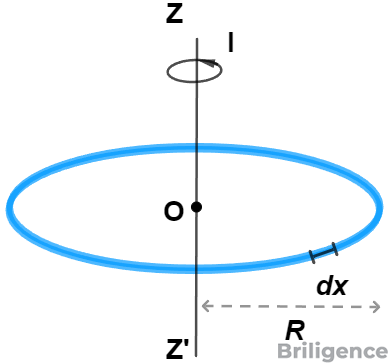
Then, mass of the elementary portion $= \dfrac{M}{2\pi R} dx$
As the ring rotates about the axis $ZZ’$, the elementary portion is always at a distance $R$ from it. Therefore, the moment of inertia of the elementary portion about $ZZ’$:
$ \displaystyle =\left( {\frac{M}{{2\pi R}}dx} \right){{R}^{2}}=\frac{M}{{2\pi }}Rdx$
The moment of inertia $I$ of the ring about axis $ZZ’$ can be found by integrating the above for the whole circumference of the ring i.e. between limits $x = 0$ to $x = 2 \pi R$:
$\displaystyle I=\int_{0}^{{2\pi R}}{{\frac{M}{{2\pi }}}}Rdx$
$ \displaystyle \Rightarrow I=\frac{M}{{2\pi }}R\left[ x \right]_{0}^{{2\pi R}}$
$ \displaystyle \Rightarrow I=\frac{M}{{2\pi }}R[2\pi R-0]$
$ \displaystyle I=M{{R}^{2}}$