Physics and Mathematics
Banking of Roads
1. Concept Introduction
When a vehicle moves along a curved road, it requires a centripetal force to stay on the curved path.
If the road is flat, this force is provided only by the friction between the tires and the road.
However, at higher speeds or on slippery roads, friction alone may not suffice.
To ensure safe turning, roads are banked — i.e., the road surface is tilted at an angle [\theta] with the horizontal.
This inclination provides a horizontal component of the normal reaction that contributes to the centripetal force, reducing dependence on friction.
2. Mathematical Derivation (Frictionless Banking)
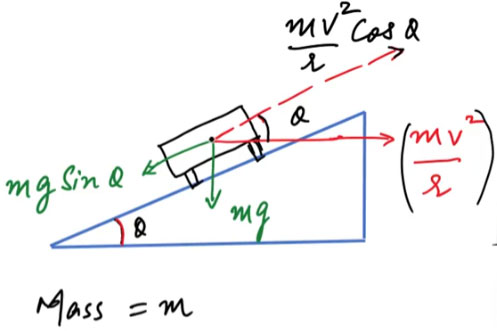
Consider a vehicle of mass [m] moving at speed [v] on a curved road of radius [r] banked at an angle [\theta].
Let the forces acting on the vehicle be:
- Normal reaction: [N] (perpendicular to the road surface)
- Weight: [mg] (vertically downward)
Resolving components:
- Along the vertical: [N\cos\theta = mg]
- Along the horizontal: [N\sin\theta = \dfrac{mv^2}{r}]
Dividing these equations:
[\tan\theta = \dfrac{v^2}{rg}]
Hence, speed for safe turn without friction is:
[v = \sqrt{rg\tan\theta}]
3. With Friction
When friction acts (say with coefficient [\mu]), the condition for maximum safe speed [v_{max}] and minimum speed [v_{min}] becomes:
[v_{max}] [= \sqrt{\dfrac{rg(\sin\theta + \mu\cos\theta)}{\cos\theta – \mu\sin\theta}}]
[v_{min}] [= \sqrt{\dfrac{rg(\sin\theta – \mu\cos\theta)}{\cos\theta + \mu\sin\theta}}]
4. Optimum Banking Angle
For a given speed [v] and curve radius [r]:
[\tan\theta = \dfrac{v^2}{rg}]
This ensures that no friction is required to negotiate the curve — all centripetal force is provided by the horizontal component of [N].
5. Forces on a Banked Turn
| Force | Direction | Function |
|---|---|---|
| [mg] | Vertically downward | Weight of vehicle |
| [N] | Perpendicular to road | Provides vertical & horizontal components |
| [f] | Along road surface | Provides additional centripetal force (if needed) |
6. Mathematical Insights
- The horizontal component of [N] provides centripetal acceleration:
[a_c = \dfrac{v^2}{r} = g\tan\theta] - The normal reaction increases with the banking angle, reducing reliance on friction.
- The geometry directly connects circular motion concepts ([v], [r], [\omega]) with trigonometric resolution of vectors.
7. Practical Examples
- Highways and Race Tracks: Banked at curves to allow high-speed turning without skidding.
- Railway Tracks: Outer rail is raised to balance centrifugal tendency.
- Cycle Racing Tracks (Velodrome): Heavily banked to allow extremely high cornering speeds.
- Airport Runways: Banked at ends for safe aircraft maneuvering.
- Mountain Roads: Often banked inward to counteract outward pseudo forces on curves.
8. Important Formulas Summary
| Quantity | Formula | Description |
|---|---|---|
| Banking angle | [\tan\theta = \dfrac{v^2}{rg}] | Frictionless condition |
| Safe speed | [v = \sqrt{rg\tan\theta}] | Optimum turning speed |
| Max speed | [v_{max} = \sqrt{\dfrac{rg(\sin\theta + \mu\cos\theta)}{\cos\theta – \mu\sin\theta}}] | With friction |
| Min speed | [v_{min} = \sqrt{\dfrac{rg(\sin\theta – \mu\cos\theta)}{\cos\theta + \mu\sin\theta}}] | With friction |
9. Solved Numerical Example
Example:
A car moves around a curve of radius [r = 50 m]. The road is banked at [\theta = 10^\circ]. Find the speed for which no friction is required. ([g = 9.8 m/s^2])
[v = \sqrt{rg\tan\theta} = \sqrt{50 \times 9.8 \times \tan 10^\circ} = 9.3 , m/s]
Hence, the vehicle can safely negotiate the curve at [9.3 , m/s] without friction.
10. Conceptual Questions
1. Why are roads banked on curves?
To provide part of the centripetal force through the normal reaction, reducing reliance on friction.
2. What would happen if roads were not banked?
Vehicles would rely entirely on friction, increasing the risk of skidding at high speeds.
3. What happens when a car moves faster than the design speed on a banked curve?
Friction acts downward along the slope to prevent outward skidding.
4. What happens when a car moves slower than the design speed?
Friction acts upward along the slope to prevent the car from sliding inward.
5. What is the advantage of a frictionless design speed?
It ensures safety even under low-friction conditions like rain or ice.
6. Does banking angle depend on vehicle mass?
No, the formula [\tan\theta = \dfrac{v^2}{rg}] is independent of mass.
7. What determines the optimum banking angle?
The intended design speed and curvature radius.
8. Why are race tracks more steeply banked than highways?
Because vehicles move at much higher speeds, requiring larger centripetal force components.
9. How does friction assist in turning on a banked curve?
Friction provides or opposes part of the centripetal force depending on the vehicle’s speed.
10. Why do trains have elevated outer rails on curves?
To generate a banking effect that counteracts outward inertia of the train.
11. What happens to normal reaction when banking angle increases?
It becomes more inclined, producing a larger horizontal component.
12. Can a flat road be safe at high speeds?
Only if friction is high enough; otherwise, banking is essential.
13. What factors affect the maximum safe speed?
Radius of curve, coefficient of friction, and banking angle.
14. What is meant by design speed?
The speed at which a vehicle can safely take a curve without relying on friction.
15. Why do vehicles skid outward on sharp turns?
Because the required centripetal force exceeds what friction or the bank can provide.
11. FAQs / Common Misconceptions
1. Does banking eliminate friction?
No, it reduces dependence on friction but does not eliminate it entirely.
2. Is the banking angle same for all roads?
No, it depends on the curve’s radius and the design speed.
3. Can the car move at any speed safely on a banked curve?
Only within a safe range; at very high or low speeds, friction is still required.
4. Why is outer edge of the road raised?
To create a bank angle that directs part of the normal reaction toward the center.
5. Does banking angle depend on vehicle mass?
No, it’s independent of mass.
6. What provides centripetal force on a banked road without friction?
The horizontal component of the normal reaction.