Physics and Mathematics
Bending of a Cyclist
1. Concept Overview
When a cyclist takes a turn on a curved path, they bend inward to balance the centripetal force required for circular motion with the component of the gravitational force.
If the cyclist doesn’t bend, an unbalanced torque would make them fall outward due to inertia (the tendency to move in a straight line).
The bending ensures that the resultant of the normal reaction [N] and weight [mg] passes through the center of gravity (C.G.) of the cyclist–bicycle system, maintaining equilibrium.

2. Derivation of Bending Angle
Let:
- [v] = velocity of the cyclist
- [r] = radius of the circular path
- [g] = acceleration due to gravity
- [θ] = angle of inclination with the vertical
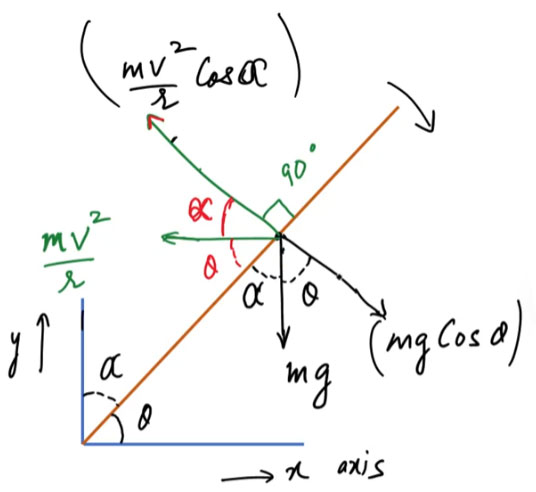
For the equilibrium of torques about the contact point,
[\tan\theta = \dfrac{v^2}{r g}]
Hence,
[\theta = \tan^{-1}\left(\dfrac{v^2}{r g}\right)]
3. Key Observations
- The faster the cyclist moves ([v ↑]), the greater the angle of bending.
- The smaller the radius of curvature ([r ↓]), the greater the angle required.
- For a flat circular track, friction provides the required centripetal force.
4. Important Formulas to Remember
| Quantity | Formula | Description |
|---|---|---|
| Centripetal Force | [F_c = \dfrac{m v^2}{r}] | Force needed to move in circular path |
| Condition for Equilibrium | [\tan\theta = \dfrac{v^2}{r g}] | Relation between speed, radius, and bend angle |
| Reaction Components | [N \cos\theta = mg], [N \sin\theta = \dfrac{m v^2}{r}] | Vertical and horizontal force balance |
| Bending Angle | [\theta = \tan^{-1}\left(\dfrac{v^2}{r g}\right)] | Determines how much the cyclist should lean |
5. Practical Examples
- Motorbike racers leaning steeply while cornering on tracks.
- Cyclists bending inward when taking sharp turns at high speed.
- Airplane pilots banking their aircraft while turning.
- Ice skaters leaning toward the center while turning.
- Cars on curved roads at high speed—though not as visible, they experience similar physics.
6. Conceptual Questions
1. Why does a cyclist bend inward while turning?
To balance the torque and ensure that the resultant of the weight [mg] and the normal reaction [N] passes through the center of gravity, preventing outward fall.
2. What would happen if a cyclist didn’t bend during a turn?
The unbalanced torque would make the cyclist fall outward due to inertia.
3. How does the radius of the circular path affect the bending angle?
A smaller radius requires a larger bending angle, as [tanθ = v² / (r g)].
4. Why is bending more pronounced at higher speeds?
Because centripetal force is proportional to [v²]; greater speed needs more inward lean to maintain equilibrium.
5. What provides the necessary centripetal force on a flat track?
The static friction between the tires and the ground provides the required centripetal force.
6. How does the cyclist ensure equilibrium while turning?
By bending such that the resultant of [N] and [mg] passes through the center of gravity.
7. What happens if the friction between tires and road is insufficient?
The cyclist will skid outward because the required centripetal force cannot be generated.
8. How is this concept similar to banking of roads?
Both involve tilting (bending or banking) to create a component of the normal force that contributes to centripetal force.
9. Why is the line of action of the resultant force important?
It must pass through the center of gravity to maintain rotational equilibrium.
10. What happens to [θ] when [v] doubles?
Since [tanθ ∝ v²], doubling [v] makes [tanθ] four times larger, increasing the bending angle.
11. Does mass affect the bending angle?
No, the angle [θ] is independent of mass; it depends only on [v], [r], and [g].
12. Can a cyclist take a turn safely if [v² > r g tanθ]?
No, the cyclist will lose balance and fall outward.
13. Why does a racing cyclist often crouch while turning?
To lower the center of gravity and increase stability during turns.
14. How does the gravitational pull affect the turning dynamics?
It acts downward and must be balanced by the vertical component of the normal reaction for equilibrium.
15. What mathematical concept underlies the relation [tanθ = v² / (r g)]?
It arises from the trigonometric relation between the horizontal and vertical components of forces.
7. FAQs / Common Misconceptions
1. Does the cyclist bend to counteract centrifugal force?
The cyclist bends inward to align the resultant of [mg] and [N] with the center of gravity. “Centrifugal force” is a pseudo force that appears in the rotating frame.
2. Is the frictional force always directed toward the center?
Yes, the static friction acts toward the center, providing the required centripetal force for circular motion.
3. Does a heavier cyclist need to bend more?
No, bending angle [θ] does not depend on mass; it depends only on [v], [r], and [g].
4. Can the cyclist take a turn on a frictionless surface?
No, without friction, there’s no centripetal force, and turning becomes impossible.
5. Is this bending concept similar to an aircraft banking?
Yes, both involve creating a component of lift or normal force toward the center of curvature for circular motion.