Physics and Mathematics
Centripetal Force – Definition, Formula and Unit
1. Concept Introduction
When an object moves along a circular path, its direction of motion continuously changes. Even if its speed remains constant, the velocity (a vector quantity) changes because its direction changes.
Hence, there must be a net force acting on the object toward the center of the circle — this force is called the Centripetal Force.
The word centripetal means “center-seeking.”
Thus, centripetal force is the force that keeps a body moving in a circular path.
2. Mathematical Expression
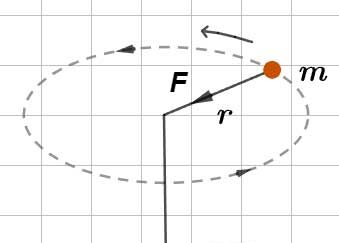
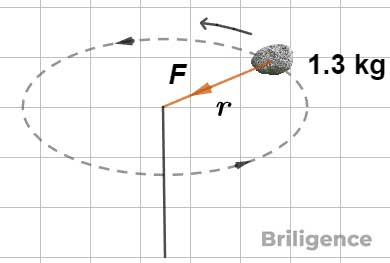
For an object of mass [m] moving with uniform speed [v] in a circular path of radius [r]:
[F = \dfrac{mv^2}{r}]
The direction of [F] is always toward the center of the circular path.
3. Relation with Angular Velocity
Since [v = \omega r],
[F = m\omega^2 r]
where [\omega] is the angular velocity in radians per second.
4. SI Unit and Dimensional Formula
| Quantity | SI Unit | Dimensional Formula |
|---|---|---|
| Centripetal Force | Newton (N) | [M^1L^1T^{-2}] |
5. Practical Examples of Centripetal Force
- Car turning on a curved road: The friction between the tires and road provides the required centripetal force.
- Planet revolving around the Sun: The gravitational force acts as the centripetal force.
- Electron revolving around the nucleus: The electrostatic force acts as the centripetal force.
- Stone tied to a string and whirled in a circle: The tension in the string provides the centripetal force.
- Cloth drying in a washing machine: Water droplets are forced out tangentially, while the drum provides centripetal force to the clothes.
6. Relation to Mathematical Concept
While deriving [F = \dfrac{mv^2}{r}], the concept of uniform circular motion involves vector components and differentiation of velocity direction with respect to time.
7. Important Formulas to Remember
| Formula | Description |
|---|---|
| [F = \dfrac{mv^2}{r}] | Basic formula for centripetal force |
| [F = m\omega^2 r] | Force in terms of angular velocity |
| [a_c = \dfrac{v^2}{r}] | Centripetal acceleration |
| [T = \dfrac{2\pi r}{v}] | Time period for one revolution |
| [v = \omega r] | Relation between linear and angular speed |
8. Practice Questions (with Solutions)
Q1. A car of mass [1000 , kg] moves with a speed of [20 , m/s] on a circular track of radius [50 , m]. Find the centripetal force.
Solution:
[F = \dfrac{mv^2}{r} = \dfrac{1000 \times 20^2}{50} = 8000 , N]
Q2. An electron moves in a circle of radius [0.5 , m] at [10 , m/s]. Find its centripetal acceleration.
Solution:
[a_c = \dfrac{v^2}{r} = \dfrac{10^2}{0.5} = 200 , m/s^2]
Q3. If a stone tied to a string of length [1.5 , m] makes 20 revolutions per second, find the required centripetal force if its mass is [0.2 , kg].
Solution:
[\omega = 2\pi \times 20 = 40\pi , rad/s]
[F = m\omega^2 r = 0.2 \times (40\pi)^2 \times 1.5 = 4740 , N]
Q4. If a car negotiates a flat curve of radius [100 , m] with a speed of [25 , m/s], find the required coefficient of friction.
Solution:
[F = \dfrac{mv^2}{r} = \mu mg]
[\Rightarrow \mu = \dfrac{v^2}{rg}] [= \dfrac{25^2}{100 \times 9.8} = 0.64]
9. Conceptual Questions
1. Why does an object moving in a circle need a force toward the center?
Because the direction of velocity keeps changing, requiring a continuous inward acceleration — hence an inward (centripetal) force.
2. Does centripetal force do work on the object?
No, because the force is always perpendicular to the direction of motion.
3. What provides the centripetal force for a satellite around Earth?
The gravitational attraction between Earth and the satellite.
4. What happens if the centripetal force is suddenly removed?
The object will move tangentially to the circular path due to inertia.
5. Is centripetal force a new kind of force?
No, it is just a name for any existing force (like tension, friction, or gravity) that acts toward the center.
6. Why does mud fly off a rotating tire?
Because the centripetal force required to keep it moving in a circle is missing, so it moves tangentially.
7. Is centrifugal force real?
No, it is a pseudo force experienced in a rotating frame of reference.
8. Why does a car skid on a sharp turn?
The frictional force available is less than the required centripetal force.
9. Does centripetal acceleration depend on mass?
No, it depends only on speed and radius ([a_c = \dfrac{v^2}{r}]).
10. Can a body in circular motion be in equilibrium?
No, because its velocity direction continuously changes — implying acceleration.
11. Why do banked roads reduce skidding?
Because a component of the normal reaction contributes to centripetal force.
12. In a rotating fan, which part experiences more centripetal force?
The tip of the blade — because centripetal force increases with radius.
13. What is the direction of centripetal acceleration?
Always toward the center of the circular path.
14. Can centripetal force change the speed of an object?
No, it only changes direction, not magnitude of velocity.
15. Is centripetal force the same as tension in a string during circular motion?
In such a case, yes — tension provides the required centripetal force.
10. FAQs / Common Misconceptions
1. Is centrifugal force the same as centripetal force?
No. Centripetal force is a real force directed towards the center. Centrifugal force is a pseudo force that appears to act outward on a body moving in a circle when viewed from the rotating frame.
2. Does centripetal force do any work on the object?
No. The centripetal force is always perpendicular to the displacement, so it does no work and doesn’t change the speed, only the direction.
3. Is tension always equal to the centripetal force?
Not necessarily. Tension provides the centripetal force in circular motion, but in cases like vertical motion, it varies because gravity also acts on the body.
4. Why do we feel an outward pull when turning in a car?
You feel inertia — your body wants to continue moving straight, while the car turns. The seat provides the inward (centripetal) force to change your direction.
5. Does higher speed always require greater centripetal force?
Yes. From [F = \dfrac{mv^2}{r}], the force increases with the square of speed for the same radius and mass.
6. Can centripetal force change the speed of the body?
No, it only changes the direction of motion. Speed remains constant in uniform circular motion.
7. What is the difference between centripetal and radial acceleration?
Centripetal acceleration is the acceleration toward the center, and its cause is the centripetal force. They are directly related by [F = ma_c].
8. Is centripetal force an additional force?
No. It’s not a new kind of force; it’s the name given to the net force responsible for circular motion, which could be tension, gravity, friction, etc.