Physics and Mathematics
First Equation of a Uniformly Accelerated Motion
1. Introduction
The first equation of motion describes the relationship between an object’s initial velocity, final velocity, acceleration, and time during uniform acceleration (constant acceleration in a straight line).
It helps us determine how the velocity of an object changes with time when subjected to uniform acceleration.
2. Statement of the First Equation of Motion
The equation is given as:
[v = u + at]
Where:
- [v] = final velocity (m/s)
- [u] = initial velocity (m/s)
- [a] = uniform acceleration (m/s²)
- [t] = time taken (s)
👉 This equation tells us that the final velocity equals the initial velocity plus the product of acceleration and time.
3. Derivation of the First Equation of Motion
(a) Using the Definition of Acceleration:
Acceleration is the rate of change of velocity with time:
[a = \dfrac{v – u}{t}]
Rearranging:
[
v – u = at
]
[v = u + at]
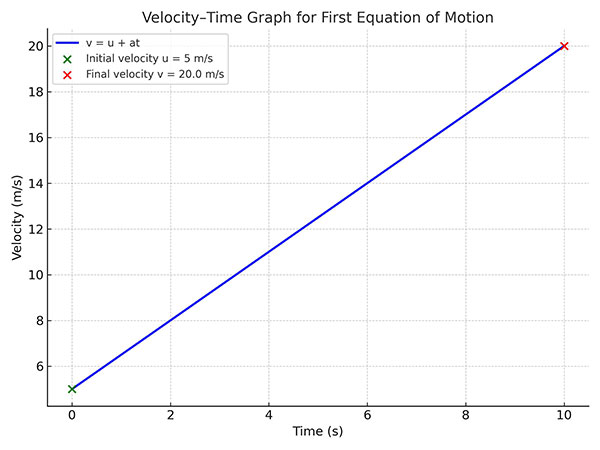
(b) Using the Graphical Method:
- Consider the velocity–time graph of an object moving with uniform acceleration.
- The graph is a straight line sloping upward, starting from the initial velocity u at time t = 0 to the final velocity v at time t.
- The slope of the velocity–time graph gives acceleration:[a = \dfrac{v – u}{t}]Rearranging, we again get:[v = u + at]
4. SI Unit and Dimensional Formula
- SI Unit of velocity (v, u): m/s
- SI Unit of acceleration (a): m/s²
- SI Unit of time (t): seconds
Dimensional formula:
[v = u + at \quad \Rightarrow \quad] [[M^0 L^1 T^{-1}]]
5. Important Formulas to Remember
| No. | Formula | Description |
|---|---|---|
| 1 | [v = u + at] | Final velocity after time [t] |
| 2 | [a = \dfrac{v – u}{t}] | Acceleration as the rate of change of velocity |
| 3 | [t = \dfrac{v – u}{a}] | Time required to change velocity |
6. Practice Questions (with Solutions)
Q1. A car starts from rest and moves with an acceleration of [2\ \text{m/s}^2] for [5\ \text{s}]. Find its final velocity.
Solution:
Given: [u = 0], [a = 2\ \text{m/s}^2], [t = 5\ \text{s}]
Using [v = u + at]:
[
v = 0 + (2)(5) = 10\ \text{m/s}
]
Q2. A body has an initial velocity of [8\ \text{m/s}] and accelerates uniformly at [3\ \text{m/s}^2] for [4\ \text{s}]. Find the final velocity.
Solution:
Given: [u = 8\ \text{m/s}], [a = 3\ \text{m/s}^2], [t = 4\ \text{s}]
[
v = u + at = 8 + (3)(4) = 20\ \text{m/s}
]
Q3. A train moving at [20\ \text{m/s}] slows down uniformly to rest in [10\ \text{s}]. Find the acceleration.
Solution:
Given: [u = 20\ \text{m/s}], [v = 0], [t = 10\ \text{s}]
Using [a = \dfrac{v – u}{t}]:
[
a = \dfrac{0 – 20}{10} = -2\ \text{m/s}^2
]
7. Conceptual Questions
1. Does the first equation apply if acceleration is not constant?
No. The first equation is valid only for uniformly accelerated (constant acceleration) motion.
2. If initial velocity is zero, what does the equation simplify to?
It simplifies to [v = at].
3. If acceleration is zero, what does the equation become?
It becomes [v = u], meaning velocity remains constant.
4. Can the equation be used for deceleration?
Yes. Use a negative value for acceleration.
5. Why is the graph of v–t linear for uniform acceleration?
Because acceleration is constant, velocity increases at a constant rate over time.
8. FAQs / Common Misconceptions
1. Is acceleration always positive in this equation?
No. It can be negative for deceleration (slowing down).
2. Can we use this equation for non-linear velocity changes?
No. The equation is derived assuming linear change in velocity.
3. Is the first equation valid in curved motion?
It applies to straight-line motion; for curved paths, vector components must be considered.
4. If time is doubled, does velocity always double?
Not necessarily. The change in velocity also depends on the acceleration.
5. Can the equation be derived without using calculus?
Yes. It can be derived graphically or using the basic definition of acceleration.