Physics and Mathematics
Impulse – Definition, Formula and Unit
1. Concept Overview
When a large force acts on a body for a very short time, it produces a significant change in momentum even though the duration is small.
This effect is known as Impulse.
Definition:
Impulse is the product of the average force and the time duration for which it acts on a body.
It provides a measure of the total effect of force during its action time.
2. Mathematical Expression
If a constant force [ F ] acts on a body for a short time interval [ \Delta t ],
then Impulse [ J ] is defined as:
[
J = F \Delta t
]
If the force varies with time, then:
[
J = \int_{t_1}^{t_2} F(t) dt
]
Hence, Impulse = Change in Momentum:
[
J = \Delta p = m v – m u
]
3. Mathematical Link (Integration in Mathematics)
Impulse is the integral of force over time, i.e., the area under the Force–Time graph.
Thus, Impulse connects Newton’s Second Law [F = dp/dt] and Integral Calculus, as:
[
J = \int F dt = \int \dfrac{dp}{dt} dt = p_2 – p_1
]
4. Physical Explanation
Even though the time of action is small, if the force is large, the change in momentum can be substantial — as seen in hitting a cricket ball or hammering a nail.
The area under the F–t graph quantifies the total impulse delivered.
5. Units and Dimensions
| Quantity | Symbol | SI Unit | Dimensional Formula |
|---|---|---|---|
| Impulse | [ J ] | N·s or kg·m/s | [ M^1L^1T^{-1} ] |
| Force | [ F ] | Newton [N] | [ M^1L^1T^{-2} ] |
| Time | [ t ] | second [s] | [ T ] |
Note that Impulse and Change in Momentum have the same units and dimensions.
6. Important Formulas to Remember
| Formula | Description |
|---|---|
| [ J = F \Delta t ] | For constant force |
| [ J = \int_{t_1}^{t_2} F(t) , dt ] | For variable force |
| [ J = \Delta p = m(v – u) ] | Relation with momentum |
| [ F = \dfrac{J}{\Delta t} ] | Average force over time |
| [ \text{Area under F–t graph} = J ] | Graphical interpretation |
7. Example Calculation
Example 1:
A constant force of 10 N acts on a body for 0.2 s. Find the impulse.
[
J = F \Delta t = 10 \times 0.2 = 2,\text{N·s}
]
Example 2:
A ball of mass 0.5 kg changes its velocity from 10 m/s to 0 in 0.1 s after hitting a wall. Find the average force.
[
J = \Delta p = m(v – u) = 0.5(0 – 10) = -5 \text{kg·m/s}
]
[
F = \dfrac{J}{\Delta t} = \dfrac{-5}{0.1} = -50 \text{N}
]
(The negative sign indicates the direction opposite to motion.)
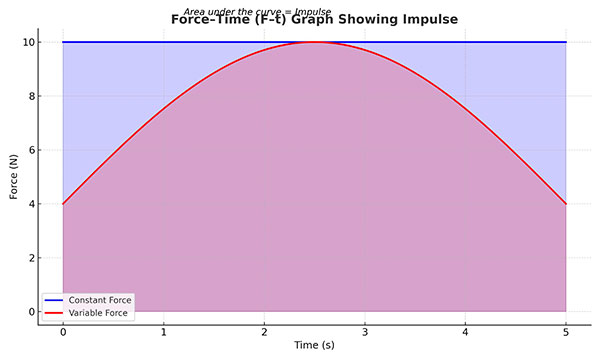
8. Graphical Representation
In the Force–Time (F–t) graph, the area under the curve represents Impulse.
- If the force is constant, the graph is a rectangle.
- If the force varies, the area under the curve still gives total impulse.
9. Practice Questions (With Solutions)
Q1. A force of 15 N acts on a body for 0.5 s. Find the impulse.
Solution:
[
J = F \Delta t = 15 \times 0.5 = 7.5,\text{N·s}
]
Q2. A ball of mass 0.2 kg moving at 20 m/s rebounds with 10 m/s in the opposite direction after collision with a wall. Find the impulse.
Solution:
[
J = m(v – u) = 0.2(-10 – 20) = -6 \text{N·s}
]
Q3. The force on a body varies with time as shown by a triangular graph [0 N at 0 s, 10 N at 2 s]. Find the impulse.
Solution:
Area of triangle = [ \dfrac{1}{2} \times 2 \times 10 = 10 \text{N·s} ]
Q4. A golf club hits a ball with an average force of 200 N for 0.01 s. Find the change in momentum.
Solution:
[
J = F \Delta t = 200 \times 0.01 = 2 \text{N·s} = \Delta p
]
Q5. The force acting on a 0.4 kg body for 0.05 s changes its velocity from 4 m/s to 8 m/s. Find the average force.
Solution:
[
J = \Delta p = m(v – u) = 0.4(8 – 4) = 1.6\text{N·s}
]
[
F = \dfrac{J}{\Delta t} = \dfrac{1.6}{0.05} = 32 \text{N}
]
10. Conceptual Questions
1. What does impulse measure physically?
The total effect of a force acting over a time interval.
2. Is impulse a scalar or vector quantity?
It is a vector quantity — same direction as the change in momentum.
3. Does impulse depend more on force or time?
It depends on both; a large force for a short time or a small force for a long time can produce equal impulse.
4. Why do athletes bend knees while landing?
To increase the time of impact and reduce the average force.
5. How is impulse related to area under the F–t graph?
The area under the Force–Time graph gives the impulse.
6. Can impulse be negative?
Yes, if the direction of force is opposite to the motion (momentum decreases).
7. What is the SI unit of impulse and why is it same as momentum?
Both are measured in N·s or kg·m/s because impulse equals change in momentum.
8. Why is catching a fast ball with a moving hand easier?
Increasing contact time reduces the average force due to \( F = \dfrac{J}{\Delta t} \).
9. Does a large impulse always mean a large force?
Not necessarily — the impulse depends on both magnitude and duration of force.
10. What mathematical concept does impulse rely on?
**Integration**, since impulse is the integral of force over time.
11. FAQs / Common Misconceptions
1. Is impulse the same as force?
No. Impulse is the product of force and time, not the instantaneous value of force.
2. Does longer contact time always reduce impulse?
No. Impulse depends on total area under the curve, not just duration.
3. Can two forces of different magnitudes produce same impulse?
Yes, if they act for different durations giving equal \( F \Delta t \).
4. Does zero impulse mean zero force?
Not necessarily; equal positive and negative forces over time can cancel out, giving zero net impulse.
5. Is impulse always positive?
No, impulse can be negative if it acts opposite to motion.