Instantaneous Acceleration

1. Introduction

When a body moves with variable acceleration, the acceleration can change at every moment of time.
The Instantaneous Acceleration of a body is defined as the acceleration of the body at a particular instant of time.

Mathematically, it is obtained by taking the derivative of velocity with respect to time:

[a_{inst} = \lim_{\Delta t \to 0} \dfrac{\Delta v}{\Delta t} = \dfrac{dv}{dt}]

👉 For a refresher on the basics of acceleration, see the Acceleration topic.
👉 For understanding how to differentiate functions, see the Differentiation topic.

2. SI Unit and Dimensional Formula

SI Unit: [m/s²]
Dimensional Formula: [M^0 L^1 T^{-2}]

3. Key Points

Instantaneous acceleration is meaningful only for motions where velocity changes with time.
If the acceleration is uniform, instantaneous acceleration = average acceleration.
In non-uniform motion, instantaneous acceleration at any time ( t ) is determined using calculus.
The slope of the velocity–time graph at any point gives the instantaneous acceleration.
Instantaneous acceleration can be positive, negative (retardation), or zero.

4. Graphical Interpretation

On a velocity–time graph, draw a tangent at the required time ( t ); the slope of this tangent gives the instantaneous acceleration at that instant.
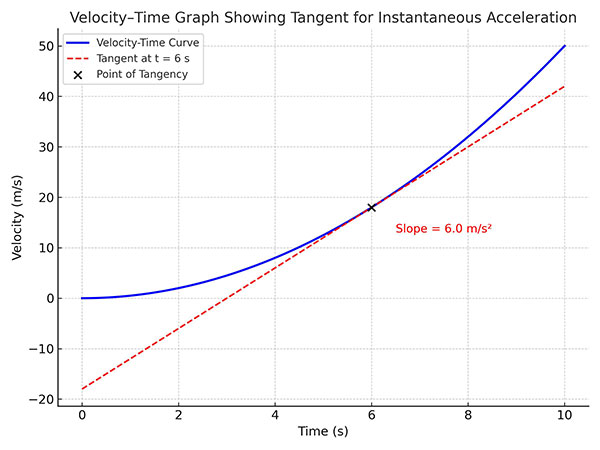
Image Credit: Ucale.org
If the slope is:
- Positive → Acceleration is positive.
- Negative → Acceleration is negative (retardation).
- Zero → No acceleration at that instant.

5. Important Formulas to Remember

No.	Formula	Description
1	[a_{inst} = \dfrac{dv}{dt}]	Instantaneous acceleration as derivative of velocity
2	[v = \dfrac{ds}{dt}]	Velocity as derivative of displacement
3	[a_{inst} = v \dfrac{dv}{ds}]	Alternate form using chain rule
4	[a_{avg} = \dfrac{\Delta v}{\Delta t}]	Average acceleration over a finite interval

👉 For how to use the chain rule in derivatives, see the Chain Rule of Differentiation topic.

6. Example Problems (With Solutions)

Velocity of a particle is given by [v(t) = 5t² + 2t]. Find its instantaneous acceleration at t = 3 s.
[
a_{inst} = \dfrac{dv}{dt} = \dfrac{d(5t^2 + 2t)}{dt} = 10t + 2
]
At [( t = 3 )] , [( a_{inst} = 10 \times 3 + 2 = 32 , \text{m/s}^2 )].
A body moves such that [s(t) = 4t³ − 3t² + 2t]. Find instantaneous acceleration at t = 2 s.
[
v(t) = \dfrac{ds}{dt} = 12t^2 – 6t + 2
]
[
a_{inst} = \dfrac{dv}{dt} = 24t – 6
]
At [( t = 2 )], [( a_{inst} = 24 \times 2 – 6 = 42 , \text{m/s}^2 )].
The velocity–time graph of a car is curved. At a certain point the tangent to the curve makes an angle of 60° with the time-axis. Find the instantaneous acceleration if the graph scale is 1 cm = 2 s on the x-axis and 1 cm = 4 m/s on the y-axis.
- Slope of tangent = tan 60° = √3
- Actual slope = (4 m/s per cm) / (2 s per cm) × √3 = 2√3 m/s².

7. Conceptual Questions (10+)

1. What is instantaneous acceleration?

It is the acceleration of a body at a specific instant of time.

2. How is instantaneous acceleration different from average acceleration?

Average acceleration is over a time interval; instantaneous acceleration is at one specific moment.

3. Can instantaneous acceleration be found graphically?

Yes, it is given by the slope of the tangent drawn to the velocity–time graph at that instant.

4. Is instantaneous acceleration always equal to dv/dt?

Yes, provided velocity is a differentiable function of time.

5. If acceleration is uniform, how does instantaneous acceleration compare with average acceleration?

They are equal because acceleration is constant at all times.

6. Can instantaneous acceleration be zero even if the body is moving?

Yes, if velocity is momentarily constant at that instant.

7. Why is calculus necessary for finding instantaneous acceleration in variable motion?

Because acceleration changes continuously and we need derivatives to calculate it at each instant.

8. Does instantaneous acceleration have direction?

Yes, it’s a vector and points in the direction of the net force.

9. Can instantaneous acceleration be negative?

Yes, if velocity decreases with time (retardation).

10. If instantaneous acceleration is zero, is the object stationary?

Not necessarily. The object could be moving at a constant velocity.

11. What does a horizontal tangent on a velocity–time graph indicate?

It indicates zero instantaneous acceleration at that point.

8. FAQs / Common Misconceptions

1. Is instantaneous acceleration the same as instantaneous velocity?

No. Instantaneous velocity is the rate of change of displacement; instantaneous acceleration is the rate of change of velocity.

2. If a body has zero instantaneous acceleration, does it stop moving?

Not necessarily; it may continue to move at constant velocity.

3. Can instantaneous acceleration be infinite?

In real physical situations, it cannot be infinite because no force changes velocity instantaneously.

4. If velocity is zero at an instant, is instantaneous acceleration also zero?

Not always. For example, at the highest point of a projectile, velocity is zero but acceleration due to gravity is not zero.

5. Does a steep tangent on a velocity–time graph mean higher instantaneous acceleration?

Yes. The steeper the tangent, the greater the instantaneous acceleration.