Physics and Mathematics
Linear Momentum and its Conservation
1. Introduction
Linear momentum is one of the most fundamental quantities in mechanics. It measures the “quantity of motion” possessed by a moving body and depends on both its mass and velocity.
2. Definition
The linear momentum of a body is defined as the product of its mass and velocity.
[p = m v]
It is a vector quantity, and its direction is the same as that of the velocity of the object.
- SI Unit: [kg·m/s]
- Dimensional Formula: [M^1 L^1 T^{-1}]
3. Relation Between Force and Momentum
From Newton’s Second Law,
[F = \dfrac{dp}{dt}]
That is, the rate of change of momentum of a body is equal to the net external force acting on it.
If the force acts for a small interval [\Delta t],
[F = \dfrac{\Delta p}{\Delta t}]
or
[\Delta p = F \Delta t]
This change in momentum is also known as Impulse.
(Related Topic Link: Impulse)
4. Law of Conservation of Linear Momentum
Statement:
If no external force acts on a system of particles, the total linear momentum of the system remains constant.
[p_{1i} + p_{2i} = p_{1f} + p_{2f}]
where subscripts i and f refer to initial and final momenta respectively.
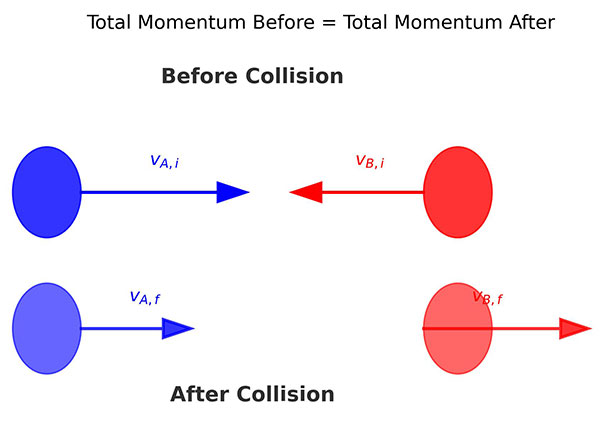
5. Derivation (Two-Body System)
Consider two bodies, [A] and [B], interacting through internal forces only.
Let [F_{AB}] be the force exerted by [A] on [B], and [F_{BA}] be the force exerted by [B] on [A].
From Newton’s Third Law,
[F_{AB} = -F_{BA}]
If the forces act for a small time [\Delta t],
[m_A \Delta v_A = -m_B \Delta v_B]
[m_A v_{A,i} + m_B v_{B,i} = m_A v_{A,f} + m_B v_{B,f}]
Thus,
[\text{Total Momentum Before}] [= \text{Total Momentum After}]
Hence, Linear Momentum is Conserved.
6. Important Formulas to Remember
| Formula | Description |
|---|---|
| [p = m v] | Linear momentum definition |
| [F = \dfrac{dp}{dt}] | Relation between force and momentum |
| [\Delta p = F \Delta t] | Impulse–momentum relationship |
| [p_{\text{initial}} = p_{\text{final}}] | Law of conservation of momentum |
7. Practical Examples
1. When a bullet is fired from a gun, the gun recoils or give a force in backward direction.
Let M be the mass of gun and m the mass of bullet. Initially, both the gun and the bullet are at rest. On firing the gun, suppose that the bullet moves with a velocity $ \displaystyle \overrightarrow{v}\text{ }$ and the gun moves with velocity $ \displaystyle \overrightarrow{V}$.
According to the principle of conservation of the momentum,
total momentum of gun and bullet before firing = total momentum of gun and bullet after firing
$ \displaystyle {\text{i}\text{.e}\text{. }0=M\vec{V}+m\vec{v}}$
$ \displaystyle {\Rightarrow \vec{V}=-\frac{m}{M}\vec{v}}$
The negative signs shows that $ \displaystyle \overrightarrow{v}\text{ and }\overrightarrow{V}$ foreign opposite direction i.e. as the bullet moves forward, the gun will move in backward direction. The backward motion of the gun is called recoil of the gun.
2. While firing a bullet, the gun must be held tight to the shoulder
Otherwise because of recoil velocity of the gun, the shoulder may get hurt. If the gun is held tight to the shoulder, then the body of the man firing the gun recoils along with the gun. As the total mass is quite large, the recoil velocity will be very small and the shoulder of the man will not get hurt.
3. When a man jumps from a boat to the shore, the both slightly moved away from the shore.
Initially, the total momentum of the boat and the man is zero. When the man jumps from the boat to the shore, total momentum of man and the boat will be zero only if the boat moves in opposite direction.
4. Rocket works on the principle of conservation of momentum.
As the fuel in the rocket undergoes combustion, the burnt gases leave the body of the rocket with the large velocity in downward direction and thus provide upward thrust to the rocket. If you assume that the fuel is burnt at a constant rate, then rate of change of momentum of the rocket will be constant. As more and more fuel gets burnt, the mass of the rocket goes on decreasing and it leads to increase of the velocity of the rocket more and more rapidly.
It may be pointed out that rocket propulsion is an application of the principal of conservation of momentum to a situation, in which the mass of the system goes on changing.
5. If an astronaut in open space, away from space safe wants to return to his spaceship, he can do so by throwing something in a direction opposite to that in which the spaceship is moving
When the is not throw some object away from the spaceship, he himself will recoil i.e. will move in opposite direction. Due to this, the astronaut will move towards the spaceship.
6. If someone left on a frictionless floor desire to get out of it, he can do so by blowing air out of his mouth.
For the reason explained above, he will move in a direction opposite to in which air is blown out by him. However, in this case the required velocity will be small and it may take him a long time to get out. If it throws away some heavy object, he can acquire comparatively large recall velocity and can get out soon.
8. Conceptual Questions
1. Can momentum be zero even if an object has mass?
Yes, if the object is at rest ([v = 0]), its momentum [p = m v = 0].
2. Is momentum always conserved?
Momentum is conserved only in isolated systems where no external forces act.
3. Can two objects with equal masses have different momenta?
Yes, if their velocities are different, their momenta will differ.
4. Why does a gun recoil backward when fired?
To conserve total momentum of the gun–bullet system. [m_g v_g = -m_b v_b].
5. If external forces act, will momentum still be conserved?
No, external forces cause a change in the total momentum of the system.
6. What happens to momentum in an inelastic collision?
Momentum is conserved, but kinetic energy is not.
7. Can a light object have more momentum than a heavy one?
Yes, if it moves with sufficiently high velocity.
8. Is impulse always equal to change in momentum?
Yes, impulse equals the total change in momentum ([J = \Delta p]).
9. If the net external force is zero, what can be said about momentum?
It remains constant according to the law of conservation of momentum.
10. How is Newton’s Second Law consistent with momentum conservation?
When [F = 0], [\dfrac{dp}{dt} = 0], meaning momentum [p] remains constant.
9. FAQs / Common Misconceptions
1. Does momentum depend only on speed?
No, it depends on both mass and velocity (a vector quantity).
2. Is momentum the same as force?
No, force is the rate of change of momentum, not the same quantity.
3. In a collision, can momentum be lost?
Not in an isolated system. However, some kinetic energy may be lost.
4. If an object’s velocity doubles, does its momentum double?
Yes, since [p = m v].
5. If an object moves in a circle at constant speed, is its momentum constant?
No, the direction changes continuously, so momentum changes.