Physics and Mathematics
Moment of inertia of a Uniform Circular Disc
Consider a circular disc of mass $M$, radius $R$, and center $O$. Then,
\[
\text{mass per unit area} = \frac{M}{\pi R^2}
\]
(i) Moment of inertia about an axis through its center and perpendicular to its plane.
Let the moment of inertia of the circular disc about the axis $ZZ’$ passing through its center $O$ and perpendicular to its plane be $I$.
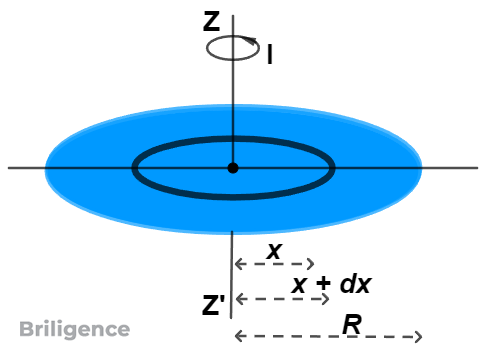
The disc can be assumed to be made up of a large number of concentric rings. Consider one such ring of radius $x$ and an infinitesimally small thickness $dx$. Then,
area of ring = circumference × width $\displaystyle =2\pi xdx$
mass of ring $\displaystyle =\frac{M}{{\pi {{R}^{2}}}}\times 2\pi xdx$ $\displaystyle =\frac{{2M}}{{{{R}^{2}}}}xdx$
Since, the moment of inertia of this ring about the axis $ZZ’$ passing through its center and perpendicular to its plane is $\displaystyle I=M{{R}^{2}}$
M.I. of ring = mass of ring × radius2
$\displaystyle =\frac{{2M}}{{{{R}^{2}}}}{{x}^{2}}dx=\frac{{2M}}{{{{R}^{2}}}}{{x}^{3}}dx$
The moment of inertia $I$ of the whole disc is the sum of the moment of inertia of all such rings, which have radii between $x = 0$ and $x = R$ and is accordingly obtained by integrating the above between the limits $x = 0$ and $x = R$.
Therefore,
\[
I = \int_0^R \frac{2M}{R^2} x^3 \, dx
\]
or
$\displaystyle I=\frac{{2M}}{{{{R}^{2}}}}\times \left[ {\frac{{{{x}^{4}}}}{4}} \right]_{0}^{R}$
$ \displaystyle \Rightarrow I=\frac{{2M}}{{{{R}^{2}}}}\times \frac{{{{R}^{4}}}}{4}=\frac{{2M}}{{{{R}^{2}}}}\times \frac{{{{R}^{4}}}}{4}$
$ \displaystyle I=\frac{{M{{R}^{2}}}}{2}$
(ii) Moment of inertia about its diameter.
As deduced in section 2.05, it can be obtained that the moment of inertia of the circular disc about its diameter:
\[
I_d = \frac{1}{2} I = \frac{1}{2} \times \left( \frac{1}{2} M R^2 \right)
\]
or
$\displaystyle {{I}_{d}}=\frac{1}{4}M{{R}^{2}}$
Example: Calculate the moment of inertia about a transverse axis through the centre of a disc, whose radius is $20 \, \text{cm}$. Its density is $9 \, \text{g cm}^{-3}$ and its thickness is $7 \, \text{cm}$.
Solution:
Here, radius of disc, $R = 20 \, \text{cm}$; thickness of disc, $t = 7 \, \text{cm}$
Density of the material of ring, $\rho = 9 \, \text{g cm}^{-3}$
Therefore, the mass of disc:
$\displaystyle M=\pi {{R}^{2}}t\rho $ $\displaystyle =\frac{{22}}{7}\times {{(20)}^{2}}\times 7\times 9\text{g}$
Moment of inertia of the disc about transverse axis (axis perpendicular to its plane) and through its center is given by
$\displaystyle \begin{array}{l}I=\frac{1}{2}M{{R}^{2}}\\=\frac{1}{2}\times \frac{{22}}{7}\times {{(20)}^{2}}\times 7\times 9\times {{(20)}^{2}}\\=1.584\times {{10}^{7}}\text{ g c}{{\text{m}}^{2}}\end{array}$