Physics and Mathematics
Moment of Inertia of a Uniform Solid Sphere about a Diameter
The moment of inertia of a uniform solid sphere of radius R and mass M is given by
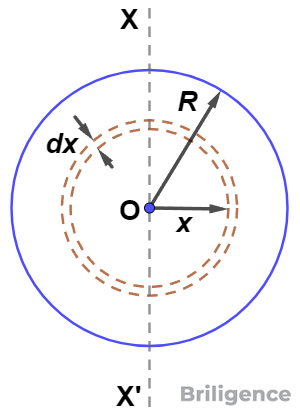
Let $M$ be the mass and $R$ be the radius of a uniform solid sphere with center $O$. We have to calculate the moment of inertia of this sphere about its diameter $XOX’$.
Volume of the solid sphere = $\dfrac{4}{3} \pi R^3$
Mass per unit volume of the solid sphere:
\[
\rho = \frac{M}{\dfrac{4}{3} \pi R^3}
\]
\[
\rho = \frac{3M}{4 \pi R^3} \tag{i}
\]
With $O$ as the center and radii $x$ and $(x + dx)$, draw two spheres within the given solid sphere. The thin spherical shell trapped between these spheres can be treated as a hollow sphere of radius $x$ and thickness $dx$.
Surface area of the elementary hollow sphere:
\[
4 \pi x^2
\]
Volume of the elementary hollow sphere:
\[
4 \pi x^2 dx
\]
Mass of the elementary hollow sphere:
\[
m = \rho (4 \pi x^2 dx)
\]
\[
m = \frac{3M}{4 \pi R^3} (4 \pi x^2 dx)
\]
\[
m = \frac{3M}{R^3} x^2 dx
\]
Moment of inertia of the elementary hollow sphere about its diameter is:
$\displaystyle dI=m{{x}^{2}}$ $\displaystyle =\left( {\frac{{3M}}{{{{R}^{3}}}}{{x}^{2}}dx} \right){{x}^{2}}$
\[
dI = \frac{3M}{R^3} x^4 dx
\]
When $x = 0$, the spherical shell is formed at the center of the solid sphere. As $x$ increases from 0 to $R$, the shells cover the entire solid sphere.
Moment of inertia of the solid sphere about its diameter is:
\[
I = \int_0^R dI = \frac{3M}{R^3} \int_0^R x^4 dx
\]
\[
I = \frac{3M}{R^3} \cdot \frac{x^5}{5} \bigg|_0^R
\]
\[
I = \frac{3M}{R^3} \cdot \frac{R^5}{5}
\]
\[
I = \frac{3M}{5} R^2
\]
$\displaystyle I=\frac{2}{5}M{{R}^{2}}$
Using the theorem of parallel axes, moment of inertia of a solid sphere about a tangent to the sphere is:
$ \displaystyle \begin{array}{l}{I}’=I+M{{R}^{2}}\\{I}’=\dfrac{2}{5}M{{R}^{2}}+M{{R}^{2}}\\{I}’=\dfrac{7}{5}M{{R}^{2}}\end{array}$