Newton’s Second Law of Motion

1. Concept Overview

Newton’s Second Law of Motion establishes a quantitative link between Force, Mass, and Acceleration, thereby defining how motion changes under an external force.

Statement:
“The rate of change of momentum of an object is directly proportional to the applied unbalanced force and takes place in the direction of the force.”

💡 Tip: Think of pushing a trolley—heavier trolleys need more force to accelerate, lighter trolleys need less. That’s the second law in action!

---

2. Mathematical Derivation

Let a body of mass ( m ) move with initial velocity ( u ).

After time ( t ), let the final velocity be ( v ).

Then, the initial momentum is:

[
p_1 = m u
]

and the final momentum is:

[
p_2 = m v
]

Change in momentum in time ( t ):

[
\Delta p = p_2 – p_1 = m(v – u)
]

Rate of change of momentum:

[
\dfrac{\Delta p}{\Delta t} = m \dfrac{v – u}{t}
]

By definition of acceleration [ a = \dfrac{v – u}{t} )],

[
\dfrac{\Delta p}{\Delta t} = m a
]

Hence,

[
\boxed{F = m a}
]

 

 

---

3. Mathematical Foundation

Here we see how Differentiation connects motion with force.
In the continuous form, Newton expressed the law as:

[
F = \dfrac{dp}{dt}
]

This is the rate of change of momentum with time.

Now, since ( p = m v ) (for constant mass systems),

[
F = m \dfrac{dv}{dt} = m a
]

So, this is a direct application of the derivative concept from calculus.
Students can explore this link further in the Mathematics section:
🔗Students can click here to revisit: Product Rule of Differentiation

---

4. Physical Explanation

• If force increases, acceleration increases proportionally (for constant mass).
• If mass increases, acceleration decreases (for constant force).
• Direction of acceleration = direction of force.

---

5. Units, Dimensions, and Definitions

Quantity	Symbol	SI Unit	Dimensional Formula
Force	( F )	Newton (N)	( M^1L^1T^{-2} )
Mass	( m )	kg	( M^1 )
Acceleration	( a )	m/s²	( L^1T^{-2} )

1 Newton (1 N) = force required to accelerate 1 kg mass by 1 m/s².

[
1,\text{N} = 1,\text{kg·m/s}^2
]

---

6. Important Formulas to Remember

Formula	Meaning / Description
[ F = \dfrac{dp}{dt} ]	General form of Newton’s 2nd Law
[ F = m a ]	Simplified form when mass is constant
[ p = m v ]	Definition of momentum
[ a = \dfrac{v – u}{t} ]	Definition of acceleration
[ F = m \dfrac{v – u}{t} ]	Alternate form connecting all quantities
[ \text{1 N} = 1 \text{kg·m/s}^2 ]	Definition of 1 Newton
[ F \propto a ] for constant [ m ]	Direct proportionality between force and acceleration
[ F \propto m ] for constant [ a ]	More mass requires more force for same acceleration

---

7. Example Calculation

A force of  [10 \text{N} ] acts on a [ 2 \text{kg} ] body.

[
F = ma \Rightarrow a = \dfrac{F}{m} = \dfrac{10}{2} = 5,\text{m/s}^2
]

Thus, acceleration = 5 m/s² in the direction of force.

---

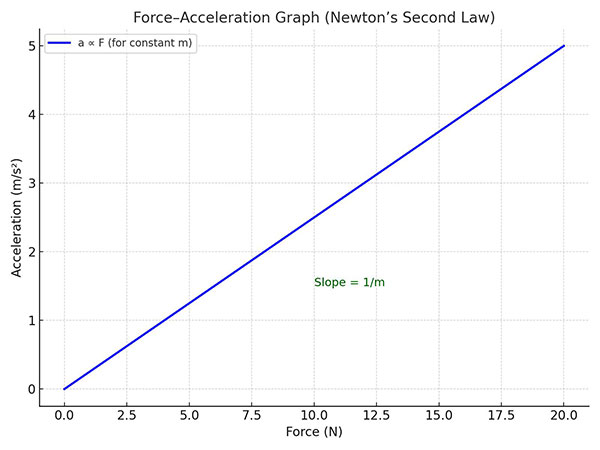
8. Graphical Interpretation

• The Force–Acceleration (F–a) graph is a straight line through the origin, showing [ a \propto F ].
• The slope of the graph gives [ \dfrac{1}{m} ].
  So, heavier objects → smaller slope (less acceleration for same force).

---

9. Practice Questions (With Solutions)

Q1. A body of mass 5 kg experiences a force of 20 N. Find its acceleration.
Solution:
[
a = \dfrac{F}{m} = \dfrac{20}{5} = 4,\text{m/s}^2
]

---

Q2. A car of mass 1000 kg increases its velocity from 10 m/s to 20 m/s in 5 s. Find the force applied.
Solution:
[
a = \dfrac{20 – 10}{5} = 2,\text{m/s}^2
]
[
F = ma = 1000 \times 2 = 2000,\text{N}
]

---

Q3. What force is required to give a 50 kg body an acceleration of 0.5 m/s²?
Solution:
[
F = ma = 50 \times 0.5 = 25,\text{N}
]

---

Q4. A constant force acts on two bodies of masses 2 kg and 4 kg. Find the ratio of their accelerations.
Solution:
[
a_1 : a_2 = \dfrac{F/m_1}{F/m_2} = \dfrac{m_2}{m_1} = 2:1
]

---

Q5. A bullet of mass 0.02 kg is fired with a force of 100 N. What is its acceleration?
Solution:
[
a = \dfrac{F}{m} = \dfrac{100}{0.02} = 5000,\text{m/s}^2
]

---

Q6. A force produces an acceleration of 2 m/s² in a 6 kg mass. What acceleration will it produce in 12 kg mass?
Solution:
[
a_2 = a_1 \dfrac{m_1}{m_2} = 2 \times \dfrac{6}{12} = 1,\text{m/s}^2
]

---

Q7. Explain mathematically how ( F = ma ) is a vector equation.
Solution:
Force and acceleration both have direction. Thus,
[
\vec{F} = m \vec{a}
]
implying both act in the same direction.

---

10. Conceptual Questions

1. What happens to acceleration if the force is doubled and mass is constant?

Acceleration doubles, since \( a \propto F \).

2. What happens if the mass is doubled but force remains constant?

Acceleration becomes half, since \( a \propto \frac{1}{m} \).

3. Why does a small bullet attain high velocity when fired?

Because its mass is very small, so even a moderate force produces very large acceleration.

4. Why is the rate of change of momentum form more general?

Because it applies even when mass is not constant (like in rockets).

5. Why does acceleration act in the direction of force?

Because force is the vector cause that changes the magnitude or direction of velocity.

6. What is the relationship between impulse and change in momentum?

Impulse \( = F \times t = \Delta p \). It’s the area under the force–time graph.

7. Can force be zero while acceleration is not?

Not in Newtonian mechanics; a ≠ 0 implies F ≠ 0.

8. How does this law explain rocket propulsion?

The expulsion of gases exerts an equal and opposite reaction, causing thrust.

9. Why is catching a ball with a moving hand easier?

Increasing time of contact decreases the force (since \( F = \frac{\Delta p}{\Delta t} \)).

10. What mathematical operation connects Newton’s Second Law to Kinematics?

**Differentiation** (rate of change of velocity or momentum with respect to time).

---

11. FAQs / Common Misconceptions

1. Is force needed to keep a body moving?

No. Only an unbalanced force can change motion, not maintain it.

2. Does zero net force mean the object is at rest?

Not necessarily; it could move with constant velocity.

3. Is force proportional to velocity?

No. It is proportional to **rate of change** of velocity — i.e., acceleration.

4. Can a large force always produce large acceleration?

Only if mass is small; for large mass, acceleration can still be small.

5. Does Newton’s Second Law hold in non-inertial frames?

No. It holds only in **inertial reference frames**.