Relation between Kinetic Energy and Linear Momentum

If a body has a mass of $ \displaystyle m$ then,

$ \displaystyle \begin{array}{l}\text{K}\text{.E}\text{.}=\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{{2m}}{{m}^{2}}{{v}^{2}}\\\Rightarrow \text{K}\text{.E}\text{.}=\dfrac{{{{p}^{2}}}}{{2m}}\end{array}$

where $ \displaystyle p$ is the linear momentum of the body i.e. $ \displaystyle p=mv$

It shows that a body cannot have kinetic energy without having linear momentum and vice-versa.

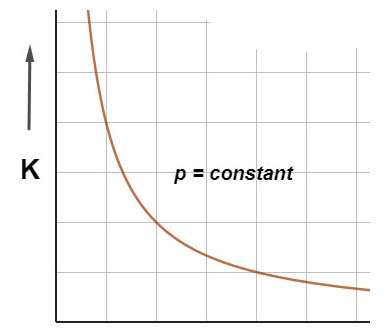
Therefore, if momentum i.e. $ \displaystyle p$ is constant the graphical representation of kinetic energy and mass is

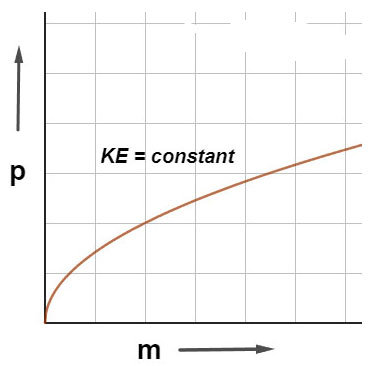
Similarly, if kinetic energy is constant, the graphical representation of kinetic momentum and mass is

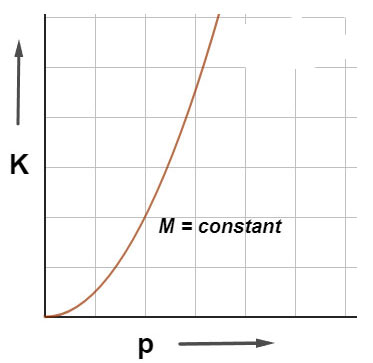
and if mass is constant, the graphical representation of kinetic energy and momentum is