Rocket Propulsion

1. Introduction

Rockets operate based on the principle of conservation of linear momentum.
When gases are expelled backward at high velocity, the rocket moves forward in response — a direct application of Newton’s Third Law of Motion.

---

2. Principle of Working

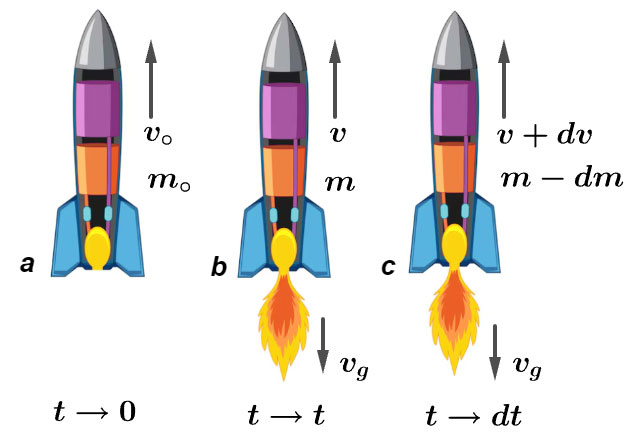
Let the rocket of mass [M] eject gases of small mass [\Delta m] with velocity [v_e] (relative to the rocket) in a short time interval [\Delta t].

Before ejection:
Total momentum = [M v]

After ejection:
Total momentum = [(M – \Delta m)(v + \Delta v) + \Delta m (v – v_e)]

Applying law of conservation of momentum:

[M v = (M – \Delta m)(v + \Delta v) + \Delta m (v – v_e)]

Neglecting higher-order small terms and simplifying, we get:

  [M , \Delta v = v_e , \Delta m]

or

[\dfrac{d v}{d t} = -\dfrac{v_e}{M} \dfrac{d M}{d t}]

This is the fundamental Rocket Equation (without external forces).

 

---

3. Derivation of the Rocket Equation (Tsiolkovsky’s Equation)

Integrating the above relation for velocity change as mass decreases from [M_0] to [M]:

[\int_{v_0}^{v} d v = -v_e \int_{M_0}^{M} \dfrac{d M}{M}]

[v – v_0 = v_e \ln \dfrac{M_0}{M}]

✅ This is known as Tsiolkovsky’s Rocket Equation, which gives the final velocity of the rocket in terms of exhaust velocity and mass ratio.

---

4. Including Gravity

When the rocket is moving vertically upward against gravity [g]:

[v = v_0 + v_e \ln \dfrac{M_0}{M} – g t]

This expression considers the retarding effect of gravity on the rocket’s velocity.

---

5. Important Formulas to Remember

Formula	Description
[F = \dfrac{dp}{dt}]	Force as rate of change of momentum
[M , dv = v_e , dM]	Basic rocket motion equation
[v – v_0 = v_e \ln \dfrac{M_0}{M}]	Tsiolkovsky’s Rocket Equation
[v = v_0 + v_e \ln \dfrac{M_0}{M} – g t]	Rocket motion under gravity
[T = \dot{m} v_e]	Thrust of the rocket (where [\dot{m}] = rate of mass ejection)

---

6. Thrust of the Rocket

The thrust is the forward force produced by the ejected gases.

[T = \dot{m} v_e]

where [\dot{m}] is the rate at which mass is expelled.

If external pressure [P_e] and atmospheric pressure [P_a] are considered,

[T = \dot{m} v_e + (P_e – P_a) A_e]

where [A_e] is the exit area of the nozzle.

 

---

7. Practical Example

Example:

A rocket expels gases at [v_e = 2000 m/s]. Initially, its mass [M_0 = 5000 kg] and final mass [M = 3000 kg].
Find the final velocity, assuming [v_0 = 0].

Solution:

[v = 2000 \ln \dfrac{5000}{3000} = 2000 \ln(1.667) = 2000 \times 0.511 = 1022 m/s]

So, the rocket reaches a velocity of approximately [1022 m/s].

 

Example:

A rocket motor consumes one quintal of fuel per second. The exhaust speed of gases w.r.t rocket is 5 km/s. Calculate the force exerted on the rocket. What is the velocity acquired by the rocket, when its mass reduces to $ \displaystyle {{\left( {\frac{1}{{100}}} \right)}^{{th}}}$ of its initial mass.

Solution:

$$\displaystyle \begin{array}{l}\text{Here, }\dfrac{{dm}}{{dt}}=1\text{ quintal/sec}\\=100\text{ kg/s}\\u=-5\text{ km/s}=-5\times {{10}^{3}}\text{ m/s}\\\text{As }F=-u\left( {\dfrac{{dm}}{{dt}}} \right)\\\therefore F=-\left( {-5\times {{{10}}^{3}}} \right)\left( {100} \right)=5\times {{10}^{5}}\text{ N}\end{array}$$

$ \displaystyle \begin{array}{*{20}{l}} {\dfrac{m}{{{{m}_{{}^\circ }}}}=\dfrac{1}{{100}}\text{ or }\dfrac{{{{m}_{{}^\circ }}}}{m}=100} \\ {\text{From }v=u{{{\log }}_{e}}\left( {\dfrac{{{{m}_{{}^\circ }}}}{m}} \right)} \\ \begin{array}{l}=5\times {{10}^{3}}{{\log }_{e}}100\\=\left( {5\times {{{10}}^{3}}} \right)\times 2.303{{\log }_{{10}}}100\end{array} \\ {=5\times {{{10}}^{3}}\times 2.303\times 2} \\ {=2.303\times {{{10}}^{4}}\text{ m/s}} \end{array}$

---

8. Conceptual Questions

1. Why does a rocket move forward when gases are expelled backward?

Because of conservation of momentum — gases gain backward momentum, and the rocket gains equal and opposite forward momentum.

2. Is the rocket pushed by air?

No, it works even in space where there is no air — it is propelled by its own exhaust gases.

3. Why does a rocket’s acceleration increase with time?

Because its mass decreases as fuel burns, so the same thrust produces greater acceleration.

4. What is exhaust velocity?

The velocity of the ejected gases relative to the rocket.

5. Does momentum conservation hold even if gravity acts?

No, gravity is an external force, so momentum is not conserved in that case.

6. Can a rocket start from rest in space?

Yes, it can, because propulsion depends on ejection of gases, not on air or ground.

7. Why is a multi-stage rocket used?

To shed unnecessary mass and improve efficiency, increasing the final velocity.

8. What happens if the exhaust velocity increases?

The rocket achieves a greater change in velocity according to [v – v_0 = v_e \ln \dfrac{M_0}{M}].

9. Is the thrust constant during motion?

Not necessarily — it depends on exhaust velocity and the rate of fuel ejection.

10. How does rocket propulsion illustrate Newton’s Third Law?

The action of gases being expelled backward produces a reaction force propelling the rocket forward.

---

9. FAQs / Common Misconceptions

1. Does a rocket push against the ground or air?

No, it pushes against its own exhaust gases; hence it works in vacuum too.

2. If no air is present, how can a rocket move in space?

The rocket moves due to conservation of momentum — not because of air resistance.

3. Does the rocket’s velocity depend on the mass of gases ejected?

Yes, velocity depends on the mass ratio [\dfrac{M_0}{M}].

4. Is a rocket more efficient at the start or end of its flight?

At the end — because its mass is lower and acceleration is higher for the same thrust.

5. Does burning fuel inside the rocket directly push it forward?

No, the rocket moves due to the reaction to the expulsion of gases, not because of combustion pressure alone.