Physics and Mathematics
Second Equation of a Uniformly Accelerated Motion
1. Introduction
The second equation of motion relates the displacement of an object to its initial velocity, time, and uniform acceleration.
It is useful for calculating how far an object travels under uniform acceleration in a straight line.
2. Statement of the Second Equation of Motion
The equation is:
[s = ut + \dfrac{1}{2} a t^2]
Where:
- [s] = displacement of the object (m)
- [u] = initial velocity (m/s)
- [t] = time taken (s)
- [a] = uniform acceleration (m/s²)
👉 This equation tells us that displacement depends on the initial motion due to [u t] and the additional distance covered due to acceleration [\dfrac{1}{2} a t^2].
👉 Click here to know more about displacement
👉 Click here to know more about uniform acceleration
3. Derivation of the Second Equation of Motion
(a) Using the Definition of Average Velocity:
The displacement is given by:
[s = \text{average velocity} \times t]
For uniform acceleration:
[
\text{average velocity} = \dfrac{u + v}{2}
]
Substitute [v = u + at]:
[
\text{average velocity} = \dfrac{u + (u + at)}{2} = u + \dfrac{1}{2}at
]
Thus:
[
s = \left(u + \dfrac{1}{2}at\right)t
]
[s = ut + \dfrac{1}{2} a t^2]
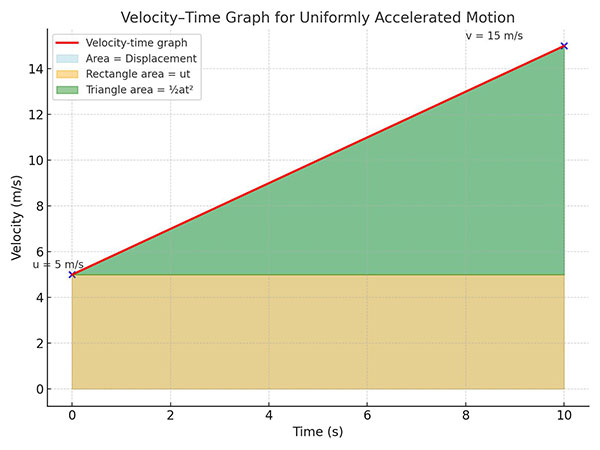
(b) Using the Graphical Method:
- In the velocity–time graph, the area under the graph gives displacement.
- For uniform acceleration, the graph is a straight line starting from u at t = 0 to v at t.
- The area under the graph is the sum of:
- Area of the rectangle: [u \times t]
- Area of the triangle: [\dfrac{1}{2}(v – u) t = \dfrac{1}{2} a t^2]
Total area:
[s = ut + \dfrac{1}{2} a t^2]
4. SI Unit and Dimensional Formula
- SI Unit of displacement ([s]): m
- SI Unit of velocity ([u]): m/s
- SI Unit of acceleration ([a]): m/s²
- SI Unit of time ([t]): s
Dimensional Formula:
[M^0 L^1 T^0]
5. Important Formulas to Remember
| No. | Formula | Description |
|---|---|---|
| 1 | [s = ut + \dfrac{1}{2} a t^2] | Displacement under uniform acceleration |
| 2 | [v = u + at] | First equation (used in derivation) |
| 3 | [a = \dfrac{v – u}{t}] | Relation between acceleration and velocity |
| 4 | [s = \dfrac{(u + v)}{2} t] | Displacement using average velocity |
6. Practice Questions (with Solutions)
Q1. A car starts from rest and accelerates uniformly at [2\ \text{m/s}^2] for [5\ \text{s}]. Find the displacement.
Solution:
Given: [u = 0], [a = 2\ \text{m/s}^2], [t = 5\ \text{s}]
[s = ut + \dfrac{1}{2} a t^2] [= 0 + \dfrac{1}{2}(2)(5^2) = 25\ \text{m}]
Q2. A train moves with an initial velocity of [20\ \text{m/s}] and accelerates at [1\ \text{m/s}^2] for [10\ \text{s}]. Find the displacement.
Solution:
Given: [u = 20\ \text{m/s}], [a = 1\ \text{m/s}^2], [t = 10\ \text{s}]
[s = ut + \dfrac{1}{2} a t^2] [= (20)(10) + \dfrac{1}{2}(1)(100) = 200 + 50 = 250\ \text{m}]
Q3. A body with initial velocity [15\ \text{m/s}] is uniformly decelerated at [2\ \text{m/s}^2] until it stops. Find the distance it covers before stopping.
Solution:
Given: [u = 15\ \text{m/s}], [v = 0], [a = -2\ \text{m/s}^2]
First, find [t]:
[t = \dfrac{v – u}{a} = \dfrac{0 – 15}{-2} = 7.5\ \text{s}]
Now:
[s = ut + \dfrac{1}{2} a t^2] [= (15)(7.5) + \dfrac{1}{2}(-2)(7.5^2)]
[s = 112.5 – 56.25 = 56.25\ \text{m}]
7. Conceptual Questions
1. Why does the second equation include a square of time?
Because the additional displacement due to acceleration increases quadratically with time.
2. What does the term [ut] represent?
It represents the displacement due to initial velocity.
3. What does the term [\dfrac{1}{2} a t^2] represent?
It represents the displacement contributed by acceleration.
4. Is the second equation valid if acceleration is not uniform?
No, it is valid only under constant acceleration.
5. If the initial velocity is zero, what does the equation simplify to?
It simplifies to [s = \dfrac{1}{2} a t^2].
6. What happens to displacement if acceleration is zero?
The equation becomes [s = ut], meaning the object moves with constant velocity.
7. Why does the graphical method use the area under the velocity–time graph?
Because the area under the velocity–time graph gives the total displacement.
8. Does negative acceleration reduce displacement?
It can reduce the displacement if it slows the object down, depending on time.
9. Can we use the second equation for vertical free-fall motion?
Yes, use [a = g] or [a = -g] depending on the direction of motion.
10. Is displacement always positive in this equation?
No. Displacement can be negative if the object moves opposite to the positive direction.
11. Why is average velocity not simply (u + v)/2 in non-uniform acceleration?
Because the second equation assumes constant acceleration; in non-uniform cases the velocity–time graph is not a straight line.
12. What does doubling time do to the displacement?
Displacement increases four times due to the [t^2] term.
13. Can displacement be zero even when there is motion?
Yes, if the object returns to its starting point.
14. If both u and a are zero, what is the displacement?
Displacement is zero because the object does not move.
15. Why is the second equation especially useful in problems of free fall?
Because it directly relates distance fallen to time under constant acceleration due to gravity.
8. FAQs / Common Misconceptions
1. Is displacement the same as distance?
No. Displacement is the shortest path from the start to end point with direction, while distance is the total path covered.
2. Can time ever be negative in the equation?
No, time is always positive in physical situations.
3. If displacement is zero, does it mean acceleration was zero?
Not necessarily; the object could have returned to its original position.
4. Does the second equation apply to non-straight-line motion?
Only in cases where motion is effectively one-dimensional.
5. Does the presence of [t^2] mean velocity is squared?
No. The [t^2] term comes from integration of velocity over time, not from squaring velocity.