Physics and Mathematics
Third Equation of a Uniformly Accelerated Motion
1. Introduction
The third equation of motion relates the square of the final velocity ([v]) of a uniformly accelerated object to its initial velocity ([u]), acceleration ([a]), and displacement ([s]).
It is given by:
[v^2 = u^2 + 2as]
This equation is extremely useful because it links velocity and displacement directly, eliminating the need for time ([t]).
2. Derivation of the Third Equation of Motion
(a) Using the First Two Equations of Motion
We know:
- First equation: ([v = u + at])
- Second equation: ([s = ut + \dfrac{1}{2}at^2])
From (1),
[
t = \dfrac{v – u}{a}
]
Substitute (t) into (2):
[s = u\left(\dfrac{v – u}{a}\right) + \dfrac{1}{2}a\left(\dfrac{v – u}{a}\right)^2]
Simplify step by step:
[s = \dfrac{u(v – u)}{a} + \dfrac{1}{2a}(v – u)^2]
[s = \dfrac{uv – u^2}{a} + \dfrac{(v^2 – 2uv + u^2)}{2a}]
[s = \dfrac{2uv – 2u^2 + v^2 – 2uv + u^2}{2a}]
[s = \dfrac{v^2 – u^2}{2a}]
Finally, multiplying both sides by (2a):
[v^2 = u^2 + 2as]
(b) Using the Graphical Method
In a velocity–time graph for uniformly accelerated motion:
- The area under the graph gives displacement (s).
- Using geometry of the trapezium, we arrive at the same result:
[
v^2 = u^2 + 2as
]
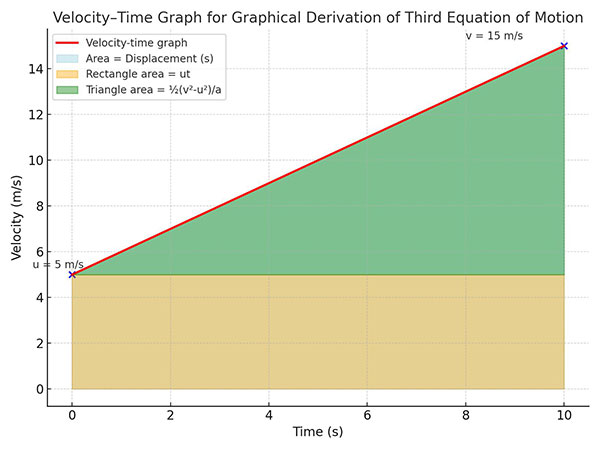
3. Conditions of Applicability
- The motion must be along a straight line.
- The acceleration must remain constant.
- The quantities (v), (u), (s), and (a) must be along the same direction.
4. SI Units and Dimensional Formula
| Quantity | SI Unit | Dimensional Formula |
|---|---|---|
| [(u, v)] (velocity) | m/s | [M⁰ L T⁻¹] |
| [a] (acceleration) | m/s² | [M⁰ L T⁻²] |
| [s] (displacement) | m | [M⁰ L T⁰] |
5. Practice Questions (With Solutions)
1. A car starts from rest and accelerates at [3\ \text{m/s}^2]. Find the velocity after it has travelled [54\ \text{m}].
Solution:
Given: [u = 0,\ a = 3\ \text{m/s}^2,\ s = 54\ \text{m}]
Using ([v^2 = u^2 + 2as]):
[
v^2 = 0 + 2 \times 3 \times 54 = 324
]
[
v = 18\ \text{m/s}
]
2. A train moving at [20\ \text{m/s}] is stopped by applying brakes after [200\ \text{m})]. Find the acceleration.
Solution:
Given: [v = 0,\ u = 20\ \text{m/s},\ s = 200\ \text{m}]
Using ([v^2 = u^2 + 2as]):
[
0 = 400 + 2a \times 200
]
[
a = \dfrac{-400}{400} = -1\ \text{m/s}^2
]
3. A ball is thrown upward with a velocity of [25\ \text{m/s}]. Find the maximum height reached. (Take [g = 9.8\ \text{m/s}^2])
Solution:
At maximum height, [v = 0,\ u = 25\ \text{m/s},\ a = -9.8\ \text{m/s}^2)]
Using ([v^2 = u^2 + 2as]):
[
0 = 625 + 2(-9.8)s
]
[
s = \dfrac{625}{19.6} \approx 31.9\ \text{m}
]
6. Conceptual Questions
1. Does the third equation of motion depend on time?
No. This equation eliminates time and relates velocity, displacement, and acceleration directly.
2. Why is the third equation useful when time is unknown?
Because it allows us to find the final velocity or displacement without needing time.
3. Can the third equation be applied if acceleration is not constant?
No. It is valid only for uniformly accelerated motion.
4. What does a negative acceleration imply in this equation?
It implies deceleration — the object is slowing down.
5. If \(v = 0\), what does the equation represent?
It represents the case when the object comes to rest after covering a certain displacement.
6. Is the displacement always positive in this equation?
Not necessarily. Displacement depends on the direction of motion and can be negative.
7. Why is this equation independent of mass?
Because in kinematics, the motion due to uniform acceleration is independent of mass.
8. Can this equation be used for vertical motion under gravity?
Yes, by replacing \(a\) with \(g\) (taking care of the sign convention).
9. If the displacement is zero, what does the equation suggest?
That the final velocity equals the initial velocity: \(v^2 = u^2\).
10. Why is the equation quadratic in nature?
Because displacement depends on the square of velocity when acceleration is constant.
11. How does the slope of the v–t graph relate to the third equation?
The slope gives acceleration, which is directly part of the equation \(v^2 = u^2 + 2as\).
12. Does the third equation imply conservation of energy?
It’s not derived from energy, but both relate because \( \dfrac{1}{2}mv^2 – \dfrac{1}{2}mu^2 = mas \).
13. Why is the graph-based derivation helpful for understanding this equation?
It visually connects the relationship between velocity, displacement, and acceleration.
14. Can the equation be used for non-linear motion?
No, it applies only to straight-line motion with constant acceleration.
15. Does this equation give the direction of motion?
No, it only gives the magnitude of velocity squared; direction must be determined separately.
7. FAQs / Common Misconceptions
1. Does higher displacement always mean higher final velocity?
Not necessarily. It depends on both displacement and the value of acceleration.
2. If acceleration is zero, does the third equation still hold?
Yes. It simplifies to \(v^2 = u^2\), meaning the velocity remains constant.
3. Can the equation be rearranged to find acceleration?
Yes. \(a = \dfrac{v^2 – u^2}{2s}\).
4. Does the third equation tell us about the time taken for the motion?
No. It eliminates time; to find time, use the first equation.