Physics and Mathematics
Uniform Acceleration
1. Introduction
A body is said to be in uniform acceleration if its velocity changes by equal amounts in equal intervals of time.
[a = \dfrac{\Delta v}{\Delta t} = \text{constant}]
Examples:
- A freely falling object under gravity.
- A car increasing its velocity steadily on a straight road.
2. SI Unit and Dimensional Formula
- SI Unit: [m/s²]
- Dimensional Formula: [M^0 L^1 T^{-2}]
3. Key Points
- Velocity changes at a uniform rate with time.
- The velocity–time graph is a straight line.
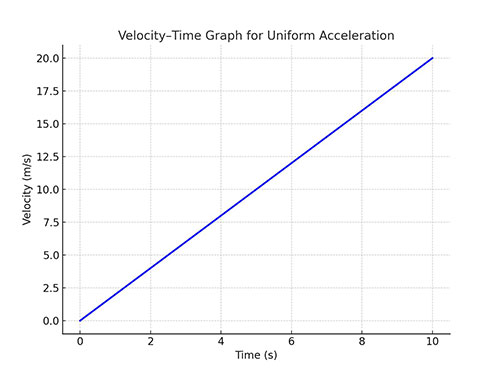
Image Credit: Ucale.org - The position–time graph is a parabola.
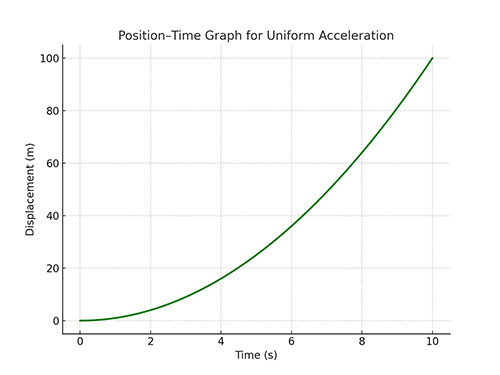
Image Credit: Ucale.org - Acceleration is constant in magnitude and direction.
- Equations of motion hold true only under uniform acceleration.
4. Derivations of the Equations of Motion
4.1 First Equation of Motion: ([v = u + at])
Statement:
Final velocity ([v]) of a body after time ([t]), starting with initial velocity ([u]), under uniform acceleration ([a]), is given by:
[v = u + at]
Derivation:
- Acceleration is the rate of change of velocity:
[
a = \dfrac{v – u}{t}
] - Rearrange:
[
v – u = at
]
[v = u + at]
✅ This shows that velocity increases (or decreases) uniformly with time.
4.2 Second Equation of Motion: ([s = ut + \dfrac{1}{2} a t^2])
Statement:
Displacement ([s]) covered by a body in time ([t]) under uniform acceleration is:
[s = ut + \dfrac{1}{2} a t^2]
Derivation (using average velocity):
- Average velocity for uniformly accelerated motion:
[
v_{avg} = \dfrac{u + v}{2}
] - Using first equation: ([v = u + at]), substitute:
[
v_{avg} = \dfrac{u + (u + at)}{2} = \dfrac{2u + at}{2} = u + \dfrac{1}{2} at
] - Displacement is average velocity × time:
[
s = v_{avg} \times t = \left(u + \dfrac{1}{2} at\right) t
]
[s = ut + \dfrac{1}{2} a t^2]
✅ This shows that displacement depends on both the initial velocity and the acceleration acting over time.
4.3 Third Equation of Motion: ([v^2 = u^2 + 2as])
Statement:
The square of the final velocity of a body moving under uniform acceleration is related to displacement ([s]) as:
[v^2 = u^2 + 2as]
Derivation (eliminating time):
- From the first equation:
[
t = \dfrac{v – u}{a}
] - Substitute into the second equation:
[
s = ut + \dfrac{1}{2} a t^2
]
[
s = u\left(\dfrac{v – u}{a}\right) + \dfrac{1}{2} a \left(\dfrac{v – u}{a}\right)^2
]
Simplify step by step:
[
s = \dfrac{u(v – u)}{a} + \dfrac{1}{2} \dfrac{(v – u)^2}{a}
]
[
s = \dfrac{u(v – u) + \dfrac{1}{2}(v – u)^2}{a}
]
Factor ((v – u)):
[
s = \dfrac{(v – u)\left[u + \dfrac{1}{2}(v – u)\right]}{a}
]
[
s = \dfrac{(v – u)\left[\dfrac{2u + v – u}{2}\right]}{a} = \dfrac{(v – u)(u + v)}{2a}
]
Multiply through:
[
2as = (v – u)(v + u)
]
[
v^2 – u^2 = 2as
]
[
v^2 = u^2 + 2as
]
✅ This relates velocity directly to displacement without involving time.
5. Important Formulas to Remember
| No. | Formula | Description |
|---|---|---|
| 1 | [a = \dfrac{\Delta v}{\Delta t}] | Definition of uniform acceleration |
| 2 | [v = u + at] | First equation of motion |
| 3 | [s = ut + \dfrac{1}{2} a t^2] | Second equation of motion |
| 4 | [v^2 = u^2 + 2as] | Third equation of motion |
| 5 | [a = \dfrac{v^2 – u^2}{2s}] | Acceleration from displacement |
| 6 | [s_n = u + \dfrac{1}{2} a (2n – 1)] | Distance covered in nth second |
6. Practice Questions
- A body starts from rest and moves with uniform acceleration 3 m/s² for 8 s. Find final velocity.
Solution: [v = u + at = 0 + 3 \times 8 = 24 , \text{m/s}] - A bus moving with 10 m/s accelerates uniformly at 2 m/s². Find distance covered in 6 s.
Solution: [s = ut + \dfrac{1}{2} a t^2 = 10 \times 6 + \dfrac{1}{2} \times 2 \times 36 = 60 + 36 = 96 , \text{m}] - A car moving at 20 m/s comes to rest after covering 40 m. Find acceleration.
Solution: [a = \dfrac{v^2 – u^2}{2s} = \dfrac{0 – 400}{80} = -5 , \text{m/s}^2] - A train accelerates from rest at 2 m/s². Find velocity after covering 100 m.
Solution: [v^2 = u^2 + 2as = 0 + 2 \times 2 \times 100 = 400 \Rightarrow v = 20 , \text{m/s}] - A body covers 19 m in the 3rd second of its motion from rest. Find its acceleration.
Solution: [s_n = u + \dfrac{1}{2} a (2n – 1) \Rightarrow 19 = \dfrac{1}{2} a (5) \Rightarrow a = \dfrac{38}{5} = 7.6 , \text{m/s}^2]
7. Conceptual Questions
1. What is uniform acceleration?
It is when velocity changes by equal amounts in equal intervals of time.
2. Does uniform acceleration always mean increasing speed?
No. It can also mean a uniform decrease in speed (retardation).
3. What is the shape of a velocity–time graph in uniform acceleration?
It’s a straight line.
4. Can uniform acceleration occur in circular motion?
No. Acceleration direction keeps changing in circular motion, so it’s not uniform.
5. Why do we get a parabola in a position–time graph for uniform acceleration?
Because displacement is proportional to t².
6. Does constant acceleration mean constant force?
Yes. According to Newton’s second law, constant acceleration implies constant net force.
7. What is the physical significance of the area under a velocity–time graph in uniform acceleration?
It represents the total displacement of the body.
8. Why are equations of motion only valid for uniform acceleration?
Because they are derived under the assumption of constant acceleration.
9. Can a stationary object have uniform acceleration?
No. It needs to start moving to have acceleration.
10. Does zero acceleration mean no motion?
No. It means the object moves with constant velocity.
11. Why is the second equation of motion quadratic in time?
Because displacement depends on t² when acceleration is constant.
8. FAQs / Common Misconceptions
1. Does uniform acceleration mean uniform velocity?
No. Uniform velocity implies no change in velocity. Uniform acceleration means velocity changes at a steady rate.
2. Can a body have uniform acceleration if it moves along a curve?
No. The direction of acceleration keeps changing in curved paths.
3. If acceleration is zero, can the body still move?
Yes. It moves with constant velocity.
4. Does uniform acceleration always increase velocity?
Not necessarily. It can also decrease velocity if acceleration is negative.
5. Is the direction of acceleration always the same as velocity?
No. When slowing down, acceleration acts opposite to velocity.