Physics and Mathematics
Variable Acceleration
1. Introduction
A body is said to be in variable (or non-uniform) acceleration when its acceleration changes with time, direction, or both.
[
a \ne \text{constant}
]
Examples:
- A car moving in heavy city traffic where the driver keeps applying brakes or accelerates irregularly.
- A swinging pendulum whose acceleration changes in magnitude and direction throughout its motion.
- A ball thrown upwards – its acceleration direction reverses after reaching the highest point.
2. SI Unit and Dimensional Formula
- SI Unit: [m/s²]
- Dimensional Formula: [M^0 L^1 T^{-2}]
3. Key Points
- The velocity–time graph is not a straight line.
- The position–time graph is generally curved and irregular.
- Equations of motion ([v = u + at]), ([s = ut + \dfrac{1}{2} a t^2]), etc., are not valid for variable acceleration.
- Instantaneous acceleration at any instant can be defined using calculus:
[
a(t) = \dfrac{dv}{dt}
]
4. Types of Variable Acceleration
- Increasing Acceleration: The rate of change of velocity increases with time (e.g., rocket take-off).
- Decreasing Acceleration: The rate of change of velocity decreases with time (e.g., a car coming to rest with gradually decreasing braking force).
- Alternating Acceleration: Acceleration changes its direction periodically (e.g., pendulum, vibrating springs).

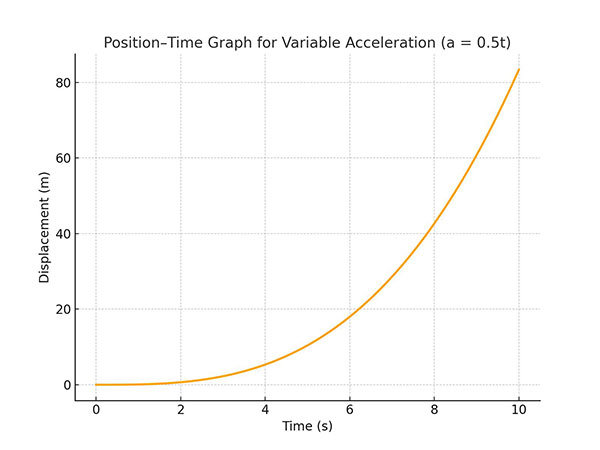
5. Important Formulas to Remember
| No. | Formula | Description |
|---|---|---|
| 1 | [a = \dfrac{dv}{dt}] | Instantaneous acceleration as the rate of change of velocity |
| 2 | [v = \dfrac{ds}{dt}] | Instantaneous velocity as the rate of change of displacement |
| 3 | [s = \int v , dt] | Displacement obtained by integrating velocity |
| 4 | [v = \int a , dt] | Velocity obtained by integrating acceleration |
| 5 | [a_{avg} = \dfrac{\Delta v}{\Delta t}] | Average acceleration over a time interval |
6. Practice Questions (With Solutions)
- A car’s velocity changes from 10 m/s to 25 m/s in the first 3 s, and then from 25 m/s to 30 m/s in the next 2 s. Calculate the average acceleration for both intervals.
- Interval 1: ([a_{avg1} = \dfrac{25 – 10}{3} = 5 , \text{m/s}^2])
- Interval 2: ([a_{avg2} = \dfrac{30 – 25}{2} = 2.5 , \text{m/s}^2])
- The acceleration of a particle moving in a straight line varies with time as [a(t) = 4t]. If v(0) = 0, find v after 5 s.
[v = \int_{0}^{5} a(t) , dt] [= \int_{0}^{5} 4t , dt = 2t^2 \bigg|_{0}^{5}] [= 2 \times 25 = 50 , \text{m/s}] - A particle moves such that [v(t) = 6t^2]. Find its displacement after 4 s (starting from rest at s = 0).
[s = \int_{0}^{4} v(t) , dt] [= \int_{0}^{4} 6t^2 , dt = 2t^3 \bigg|_{0}^{4}] [= 2 \times 64 = 128 , \text{m}] - A pendulum has acceleration given by [a = -16s], where s is displacement. What is the nature of this motion?
→ The acceleration is proportional to and opposite to displacement → Simple Harmonic Motion (oscillatory). - A car decelerates non-uniformly such that its velocity decreases from 20 m/s to 0 in 10 s. What is the average acceleration?
[a_{avg} = \dfrac{0 – 20}{10} = -2 , \text{m/s}^2 ]
7. Conceptual Questions (10+)
1. What is variable acceleration?
It is when the acceleration of a body changes with time or direction or both.
2. Can a body moving in a straight line have variable acceleration?
Yes. If its velocity doesn’t change uniformly with time, the acceleration is variable.
3. How do we find instantaneous acceleration in variable acceleration?
By using calculus: a(t) = dv/dt.
4. Can equations of motion (v = u + at) be applied in variable acceleration?
No. These equations are valid only when acceleration is constant.
5. Does variable acceleration always mean increasing velocity?
No. The velocity could also decrease depending on the direction of acceleration.
6. Why is the velocity–time graph curved in variable acceleration?
Because velocity does not change uniformly with time.
7. What does the slope of a velocity–time graph represent?
It represents the instantaneous acceleration at that point.
8. Can a body have zero velocity but variable acceleration?
Yes. For example, at the highest point of a projectile, velocity is zero but acceleration (gravity) is still acting.
9. Is acceleration always along the direction of motion?
No. It can be opposite to velocity (deceleration) or at an angle (like in circular motion).
10. Why do we use calculus for solving variable acceleration problems?
Because acceleration changes continuously with time or position, and integration/differentiation handles continuous changes.
11. Can a moving object experience variable acceleration but constant speed?
Yes. In uniform circular motion, speed is constant but direction changes, so acceleration varies.
8. FAQs / Common Misconceptions
1. Is variable acceleration the same as increasing acceleration?
No. Variable acceleration can increase, decrease, or even alternate direction.
2. If acceleration is variable, does that mean the object’s speed always fluctuates?
Not necessarily. It depends on how acceleration acts relative to velocity.
3. If acceleration changes sign, what does it mean?
It means the direction of acceleration has reversed.
4. Can average acceleration be zero even if instantaneous acceleration is not zero?
Yes. If acceleration alternates symmetrically over time, their net effect can cancel out.
5. Do we always need calculus for variable acceleration problems?
Not always. If given data at discrete time intervals, we can use algebraic or graphical methods.