Physics and Mathematics
Variable Speed
1. Definition
An object is said to have variable speed (or non-uniform speed) if it covers unequal distances in equal intervals of time, or equal distances in unequal intervals of time.
[\text{Variable Speed} \Rightarrow \dfrac{\Delta s_1}{\Delta t} \ne \dfrac{\Delta s_2}{\Delta t}]
- In this case, the speed changes with time.
- Example: A car in city traffic often accelerates and slows down, thus having a variable speed.
2. SI Unit
[\text{SI Unit of Speed} = \text{metre per second (m·s}^{-1})]
3. Dimensional Formula
[\text{Variable Speed}] = [M^{0} L^{1} T^{-1}]
4. Key Features
- Distance covered per unit time is not constant.
- There is generally non-zero acceleration.
- Position–Time graph is not a straight line; slope varies with time.
- Speed–Time graph shows changing values, often with slanted or curved lines.
5. Mathematical Expressions
- Average Speed:
For a body with variable speed over total distance [s] in time [t]:
[v_{avg} = \dfrac{\text{Total Distance Travelled}}{\text{Total Time Taken}}] - Instantaneous Speed:
The speed at a particular instant of time:
[v = \lim_{\Delta t \to 0} \dfrac{\Delta s}{\Delta t} = \dfrac{ds}{dt}]
6. Graphical Representation
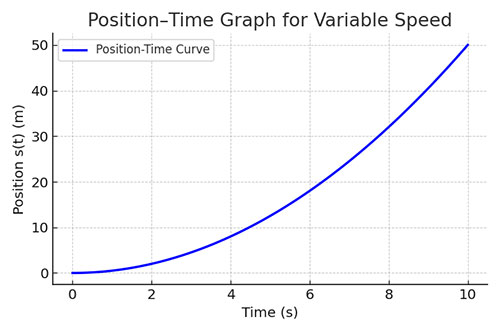
- Position–Time Graph: Curved line (changing slope).
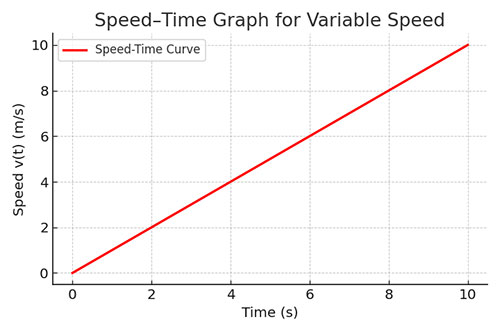
- Speed–Time Graph: Either inclined or curved, showing changing speed values.
7. Practice Questions
Solved Examples
Q1. A car covers 30 km in the first hour and 50 km in the next hour. Find the average speed.
Solution:
[v_{avg} = \dfrac{\text{Total Distance}}{\text{Total Time}} = \dfrac{30+50}{2} = 40\text{km/h}]
Q2. A body covers the first half of the distance at 20 m/s and the second half at 30 m/s. Find the average speed.
Solution:
Let total distance = 2d → each half = d.
Time in first half: [t₁ = \dfrac{d}{20}]
Time in second half: [t₂ = \dfrac{d}{30}]
Total distance = [2d], Total time = [\dfrac{d}{20} + \dfrac{d}{30} = \dfrac{5d}{60}]
[v_{avg} = \dfrac{2d}{(5d/60)} = 24\text{m/s}]
Q3. A bus moves with 12 m/s for 100 s and then 8 m/s for the next 50 s. Find its average speed.
Solution:
Total distance = [12×100 + 8×50 = 1200 + 400 = 1600\text{m}]
Total time = [100 + 50 = 150\text{s}]
[v_{avg} = \dfrac{1600}{150} \approx 10.67\text{m/s}]
Q4. If the instantaneous speed of a car increases from 0 to 25 m/s in 10 s, what is the average speed during this interval (assuming uniform acceleration)?
Solution:
For uniform acceleration, [v_{avg} = \dfrac{v_{initial} + v_{final}}{2}]
[v_{avg} = \dfrac{0 + 25}{2} = 12.5\text{m/s}]
Conceptual Questions (With Answers)
1. Define variable speed.
An object has variable speed if it covers unequal distances in equal intervals of time or equal distances in unequal intervals of time.
2. What is the SI unit and dimensional formula of variable speed?
SI Unit: m·s⁻¹
Dimensional Formula: [M⁰ L¹ T⁻¹]
3. How does the position–time graph look for variable speed?
It is curved, showing a changing slope at different points.
4. How does the speed–time graph look for variable speed?
It is slanted or curved, reflecting changes in speed over time.
5. Differentiate between average and instantaneous speed.
Average speed: total distance ÷ total time.
Instantaneous speed: speed at a particular instant, v = ds/dt.
6. Can a body have zero instantaneous speed but non-zero average speed?
Yes. For example, at the turning point in a swing, instantaneous speed is zero but average speed over the journey is not zero.
7. Is variable speed always associated with acceleration?
Generally yes, since a change in speed implies acceleration.
8. A car moves in traffic, often accelerating and decelerating. What type of speed does it have?
Variable speed.
9. A body moves 50 m in the first 5 s and 60 m in the next 5 s. Is the speed uniform or variable?
Variable, since equal time intervals cover unequal distances.
10. Give two examples of variable speed from daily life.
(i) A runner in a 100-m race who starts slow, speeds up, then slows at the finish.
(ii) A car driving through hilly terrain.
8. Common Misconceptions / FAQs
1. Does variable speed always mean changing direction?
No. Speed can vary even in straight-line motion when the rate of covering distance changes.
2. If speed varies but direction remains constant, is velocity constant?
No. Velocity changes whenever either speed or direction changes.
3. If the speed of an object doubles, does the distance covered in equal time also double?
Yes, provided the time interval remains constant.
4. If instantaneous speed is zero at some point, does it mean the object was stationary the whole time?
No. It could just be momentarily at rest (like at the highest point of a ball’s flight).